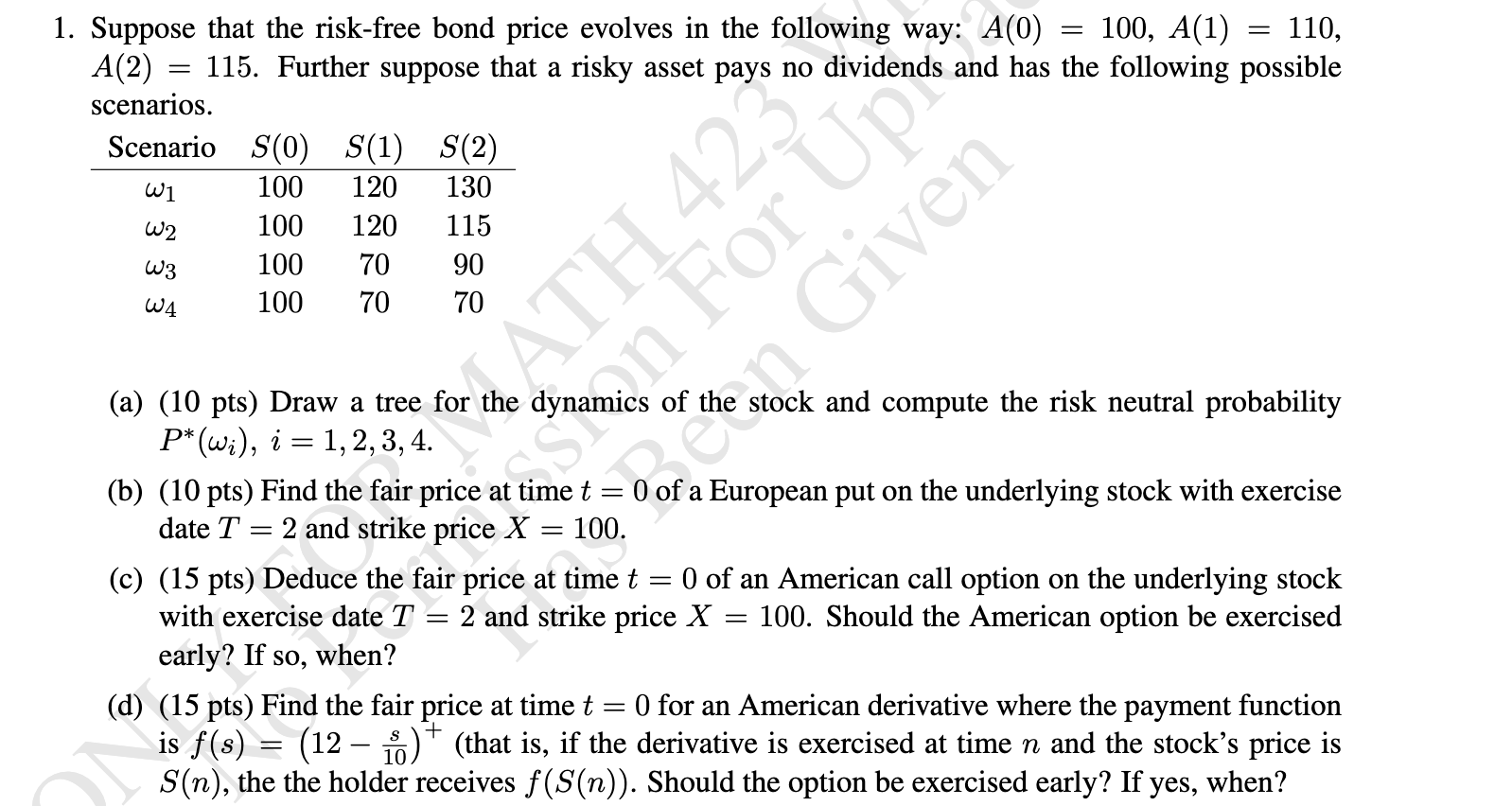
= = 1. Suppose that the risk-free bond price evolves in the following way: A(0) 100, A(1) 110, A(2) = 115. Further suppose that a risky asset pays no dividends and has the following possible scenarios. Scenario S(0) S(1) S(2) W1 100 120 130 W2 100 120 115 100 70 90 100 70 70 W3 W4 en For U APREL ATH 42 = (a) (10 pts) Draw a tree for the dynamics of the stock and compute the risk neutral probability P* (wi), i = 1, 2, 3, 4. (b) (10 pts) Find the fair price at time t = 0) of a European put on the underlying stock with exercise date T = 2 and strike price X 100. (c) (15 pts) Deduce the fair price at time t 0 of an American call option on the underlying stock with exercise date T = 2 and strike price X = 100. Should the American option be exercised early? If so, when? (d) (15 pts) Find the fair price at time t = 0 for an American derivative where the payment function is f(s) = (12 - 0) (that is, if the derivative is exercised at time n and the stocks price is S(n), the the holder receives f(S(n)). Should the option be exercised early? If yes, when? = 10 e = = 1. Suppose that the risk-free bond price evolves in the following way: A(0) 100, A(1) 110, A(2) = 115. Further suppose that a risky asset pays no dividends and has the following possible scenarios. Scenario S(0) S(1) S(2) W1 100 120 130 W2 100 120 115 100 70 90 100 70 70 W3 W4 en For U APREL ATH 42 = (a) (10 pts) Draw a tree for the dynamics of the stock and compute the risk neutral probability P* (wi), i = 1, 2, 3, 4. (b) (10 pts) Find the fair price at time t = 0) of a European put on the underlying stock with exercise date T = 2 and strike price X 100. (c) (15 pts) Deduce the fair price at time t 0 of an American call option on the underlying stock with exercise date T = 2 and strike price X = 100. Should the American option be exercised early? If so, when? (d) (15 pts) Find the fair price at time t = 0 for an American derivative where the payment function is f(s) = (12 - 0) (that is, if the derivative is exercised at time n and the stocks price is S(n), the the holder receives f(S(n)). Should the option be exercised early? If yes, when? = 10 e