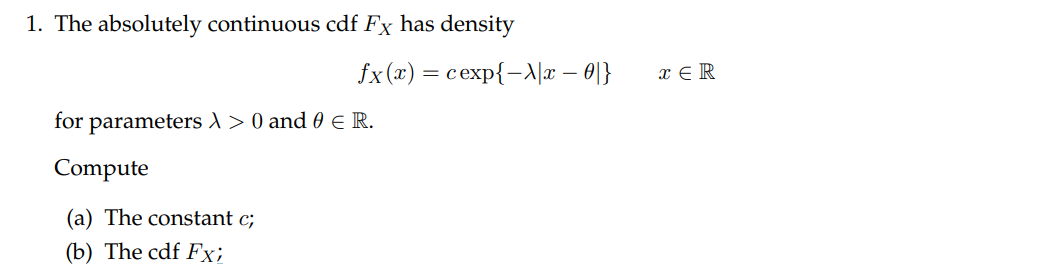
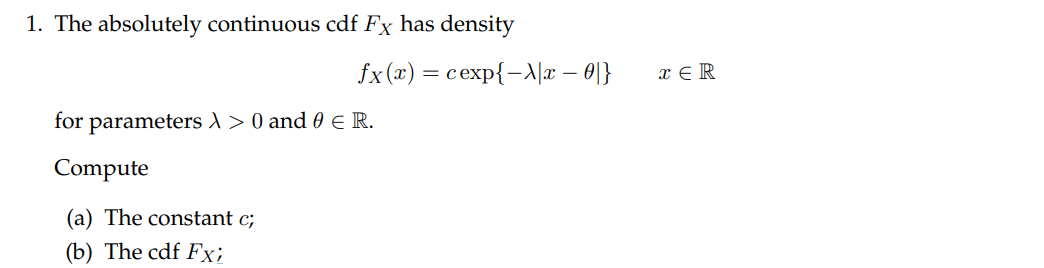
1. The absolutely continuous cdf Fx has density fx(x) = cexp{-X/x - 0/} TER for parameters > > 0 and 0 E R. Compute (a) The constant c; (b) The cdf Fx;MATH 556 - EXERCISES 1-SOLUTIONS 1. (a) The density must integrate to 1. By elementary calculations exp{-Xx - Of} dr = exp{-Xz[ } dz =2 /exp{->z} dz first by making the change of variables from r to z = r-0, and then noting that the resulting integrand is an integrable even function around zero. Thus the integral equals 2/1, so we must have c = >/2 (b) The cdf takes slightly different forms either side of 0. First, note that the density is symmetric about / so we have (1 - exp{)(x-0) } +0 Fx(@) = 191 # 191H 191 # 19/# + (1 - exp{-X(x -0)} = >0