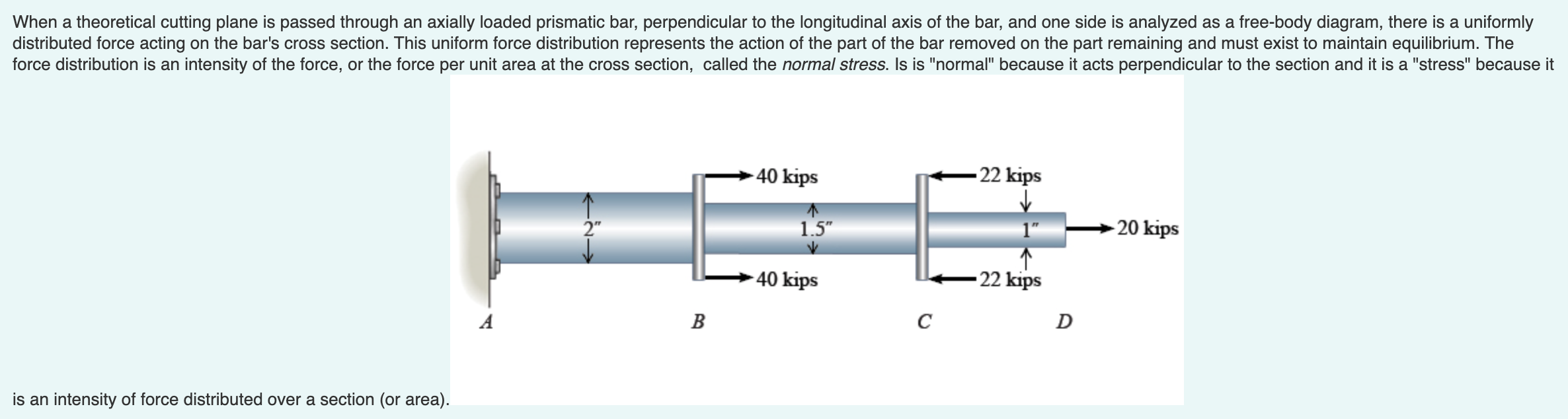
$1)$The axially loaded bar is fixed at A and loaded as shown. Draw a free$-$body diagram and determine the support reaction at A$.$ On paper, draw a free$-$body diagram of the bar and determine the reaction at A for the bar to be in equilibrium. Assume that the unknown reaction at A acts in the negative x direction. When a theoretical cutting plane is passed through an axially loaded prismatic bar, perpendicular to the longitudinal axis of the bar, and one side is analyzed as a free$-$body diagram, there is a uniformly

distributed force acting on the bar's cross section. This uniform force distribution represents the action of the part of the bar removed on the part remaining and must exist to maintain equilibrium. The

force distribution is an intensity of the force, or the force per unit area at the cross section, called the normal stress. Is is "normal" because it acts perpendicular to the section and it is a "stress" because it

is an intensity of force distributed over a section $($or area$).$

Express your answer in kips

to three significant figures.

$2)$Using the answer from Part A$,$ draw free$-$body diagrams or a load diagram and determine the internal axial forces in segments AB$,$ BC$,$ and CD$.$

Express your answer to three significant figures separated by commas.

$3)$ Using the internal axial forces determined in Part B$,$ calculate the bar's maximum average normal stress. Using your free$-$body diagrams or load diagram from Part B and the axial stress equation, calculate the bar's maximum average normal stress.

Express your answer in ksi

to three significant figures.