Question: 1. The discrete random variables $X$ and $y$ have joint distribution begin{tabular}{cccc) & $x=1$ & $x=2$ & $x=3$ hline$y=1$ & $3 / 12$ & $1

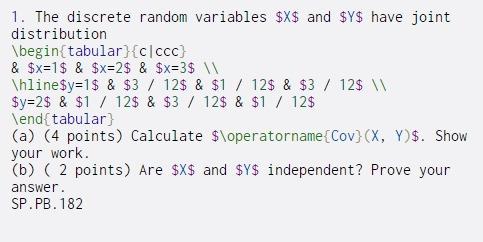
1. The discrete random variables $X$ and $y$ have joint distribution

1. The discrete random variables $X$ and $y$ have joint distribution \begin{tabular}{cccc) & $x=1$ & $x=2$ & $x=3$ \hline$y=1$ & $3 / 12$ & $1 / 12$ & $3 / 12$ $y=2$ & $1 / 12$ & $3 / 12$ & $1 / 12$ \end{tabular) (a) (4 points) Calculate $\operatorname(Cov}(X, Y)$. Show your work (b) ( 2 points) Are $X$ and $y$ independent? Prove your answer. SP.PB. 182

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Kessler Brothers produces products for farms and ranches. The administrative and manufacturing operations occupy the same 240,000-square-foot building. The manufacturing plant uses 180,000 square...

write the correct answer. A. Directions: Determine whether the items are discrete or continuous random variables. Write D if the random variable is discrete, and C if it is continuous. The...

Read and analyze the problems, show your solution, and box the answer. A. identify whether the following are discrete or continuous random variable, 1. Number of students present 2. Weight of...

Detailed answers. Problem 34.\" A spider and a y move along a straight line. At each second, the y moves a unit step to the right or to the left with equal probability p, and stays where it is with...

Section 4.1 Sections 4 .1 & 4.2: Discrete Random Variables Score: 18/69 6/23 answered Question 7 Determine the required value of the missing probability to make the distribution a discrete...

1. The discrete random variables Xo, X, and X have the following joint distribution: For Xo = 2: X 2 4 6 1 X 3 5 30 60 60 20 T 60 60 20 For Xo = 5: X 2 4 6 1 18 1 18 X1 3 2010 5 36 36 36 36 where the...

Major distributors Sections 4 .1 & 4.2: Discrete Random Variables Score: 18/69 6/23 answered .Question 9 Changing major distribution. Data were collected from a survey given to graduating college...

1. The discrete random variables $X$ and $y$ have joint distribution \begin{tabular}{1ccc} & $x=1$ & $x=2$ & $x=3$ \hline$y=1$ & $3 / 12$ & $1 / 12$ & $3 / 12$ $y=2$ & $1 / 12$ & $3 / 12$ & $1 / 12$...

1. The discrete random variables $X$ and $y$ have joint distribution \begin{tabular}{cccc} & $x=1$ & $x=2$ & $x=3$ \hline$y=1$ & $3 / 12$ & $1 / 12$ & $3 / 12$ $y=2$ & $1 / 12$ & $3 / 12$ & $1 / 12$...

Helpful hint: The following topics/concepts are covered in this homework, in no particular order (different problems cover different concepts): Class 6: Discrete Probability Distributions The...

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

Calcor Company has been a wholesale distributor of automobile parts for domestic automakers for 20 years. Calcor has suffered through the recent slump in the domestic auto industry, and its...

I. Journalize the following transactions: 1. Madison Co. purchased $225,500 of raw materials on account. 2. Actual manufacturing overhead costs include: Utilities : $2,800 a b. Depreciation on...

WHICH OF THE FOLLOWING TEMPORARY DIFFERNCES RESULTS IN A FUTURE TAXABLE AMOUNT? A SUBSCRIPTIONS RECEIVED IN ADVANCE B ESTIMATED LIABILITIES RELATED TO DISCOUNTED OPERATIONS OR RESTRUCTURINGS C SALES...

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

=+What forms of industrial action are common?

=+If there are disagreements over the meaning or application of the terms of the contract, how are they determined?

=+ Does the government play an active role in negotiations? Strikes and