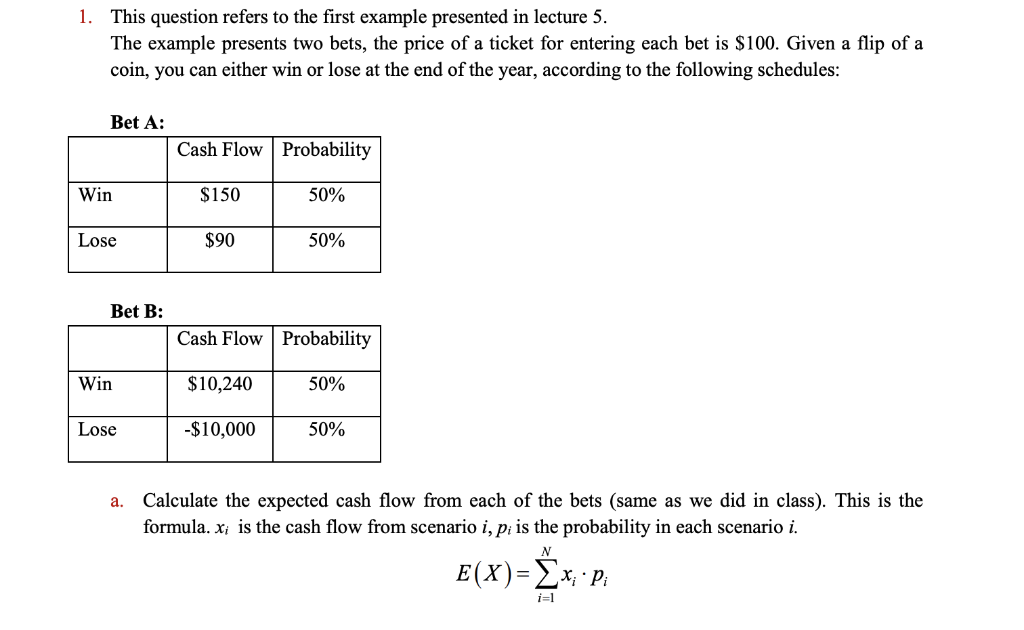
1. This question refers to the first example presented in lecture 5 The example presents two bets, the price of a ticket for entering each bet is S100. Given a flip of a coin, you can either win or lose at the end of the year, according to the following schedules: Bet A: Cash Flow| Probability Win $150 50% Lose $90 50% Bet B: Cash Flow| Probability $10,240 | 50% -$10,000| 50% Win Lose a. Calculate the expected cash flow from each of the bets (same as we did in class). This is the formula. Xi s the cash flow from scenario i, Pi is the probability in each scenario. b. Calculate the standard deviation of the cash flows in each of the alternatives. Hint Use the following formula for SD. This formula calculates SD for a situation where we have cash flows and probabilities (aka probability distribution) like in the above tables. E(X) is the expected cash flow as calculated in section a. Pi is the probability in each scenario i (win / lose) x,-E(X) *p i=1 Explain how this example of two bets is analogical to two risky projects that we may consider investing n c. d. Calculate the IRR of each of the two bets/projects, given the investment and the expected future cash flow e. The following tables (two different scenarios - table 1 and table 2) present values for cost of capital (discount rate) for each of these "projects". Explain why the values in the tables do not make sense and must be wrong. In your answer compare the alternative of investing in bet A, bet B and a risk free bank deposit with return rate of 5% (as given in the original example) Table 1 Bet A Bet B Cost of Capital 18% 12% Table 2 Bet ABet B Cost of Capital | 3% I 5% f. The following tables (two different scenarios - table 3 and table 4) present values for the cost of capital (discount rate) for each of these "projects". Compute the NPV of A and B in each of the tables and choose the best project in each scenario Table 3 Bet ABet B Cost of Capital 12% 18% Table 4 Bet ABet B Cost of Capital 12% 40% Why do you choose the less risky project in this example? Does this mean that in any situation investors always choose the less risky asset? g. 1. This question refers to the first example presented in lecture 5 The example presents two bets, the price of a ticket for entering each bet is S100. Given a flip of a coin, you can either win or lose at the end of the year, according to the following schedules: Bet A: Cash Flow| Probability Win $150 50% Lose $90 50% Bet B: Cash Flow| Probability $10,240 | 50% -$10,000| 50% Win Lose a. Calculate the expected cash flow from each of the bets (same as we did in class). This is the formula. Xi s the cash flow from scenario i, Pi is the probability in each scenario. b. Calculate the standard deviation of the cash flows in each of the alternatives. Hint Use the following formula for SD. This formula calculates SD for a situation where we have cash flows and probabilities (aka probability distribution) like in the above tables. E(X) is the expected cash flow as calculated in section a. Pi is the probability in each scenario i (win / lose) x,-E(X) *p i=1 Explain how this example of two bets is analogical to two risky projects that we may consider investing n c. d. Calculate the IRR of each of the two bets/projects, given the investment and the expected future cash flow e. The following tables (two different scenarios - table 1 and table 2) present values for cost of capital (discount rate) for each of these "projects". Explain why the values in the tables do not make sense and must be wrong. In your answer compare the alternative of investing in bet A, bet B and a risk free bank deposit with return rate of 5% (as given in the original example) Table 1 Bet A Bet B Cost of Capital 18% 12% Table 2 Bet ABet B Cost of Capital | 3% I 5% f. The following tables (two different scenarios - table 3 and table 4) present values for the cost of capital (discount rate) for each of these "projects". Compute the NPV of A and B in each of the tables and choose the best project in each scenario Table 3 Bet ABet B Cost of Capital 12% 18% Table 4 Bet ABet B Cost of Capital 12% 40% Why do you choose the less risky project in this example? Does this mean that in any situation investors always choose the less risky asset? g