Question: 1) Use a software program or graphing utility to solve the system of linear equations. (If there is no solution, enter NO SOLUTION. If the
1)
Use a software program or graphing utility to solve the system of linear equations. (If there is no solution, enter NO SOLUTION. If the system has an infinite number of solutions, set x3 = t and solve for x1 and x2 in terms of t.)
1/2x1?3/7x2+2/9x3=313/630
2/3x1+4/9x2?2/5x3=1/9
4/5x1?1/8x2+4/3x3=703/600
(x1, x2, x3) =
2)
Determine the value(s) of k such that the system of linear equations has the indicated number of solutions. (Enter your answers as a comma-separated list.)
Infinitely many solutions
16x+ky=20
kx+y=?5
k =
3)
Determine the value(s) of k such that the system of linear equations has the indicated number of solutions. (Enter your answers as a comma-separated list.)
No solution
x+ky=4
kx+y=7
k =
4)
Complete the following for the system of equations.
4x ? 8y=7
1.2x ? 2.4y=2.1
(a) Use a graphing utility to graph the equations in the system.
(b) Use the graphs to determine whether the system is consistent or inconsistent.
consistent
inconsistent
(c) If the system is consistent, approximate the solution. (If the system is inconsistent, enter INCONSISTENT. If the system has an infinite number of solutions, express x and y in terms of the parameter t.)
(x, y) ?
(d) Solve the system algebraically. (If the system is inconsistent, enter INCONSISTENT. If the system has an infinite number of solutions, express x and y in terms of the parameter t.)
(x, y) =
(e) Compare the solution in part (d) with the approximation in part (c). What can you conclude?
The system is consistent and the solutions are the same.
The system is consistent but the solutions are different.
The system is inconsistent.
4)
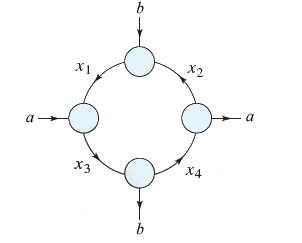
The figure given below shows the flow of traffic (in vehicles per hour) through a network of streets. (Assume a = 300 and b = 500.)
(a) Solve this system for xi, i = 1, 2, 3, 4.
(If the system has an infinite number of solutions, express x1, x2, x3, and x4 in terms of the parameter t.)
(x1, x2, x3, x4) =
(b) Find the traffic flow when x4 = 0.
(x1, x2, x3, x4) =
(c) Find the traffic flow when x4 = 300.
(x1, x2, x3, x4) =
(d) Find the traffic flow when x1 = 2x2
(x1, x2, x3, x4) =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


