Question: 1) Use the trapezoidal rule to approximate fox dx, using three non-uniform partitions at {0, 0.25, 1.5, 2}. O (03 + 0.253)(1) + (0.253 +
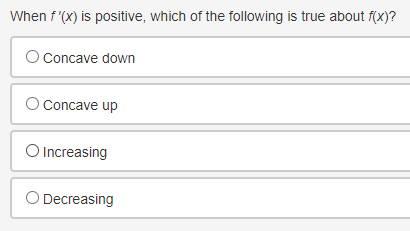

![(0.253 + 1.53)(0.5) + (1.53 + 23)(0.5)] O (03 + 0.253)(0.25) +](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667e115b6bf4d_011667e115b51389.jpg)
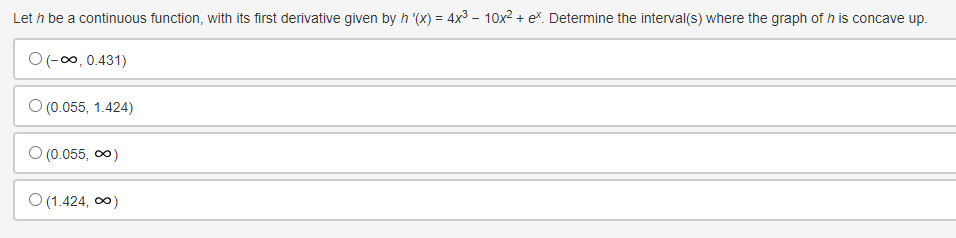
![(0.253 + 1.53)(1.25) + (1.53 + 23)(0.5)]Selected values of f ' and](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667e115bf3360_011667e115bdb68a.jpg)
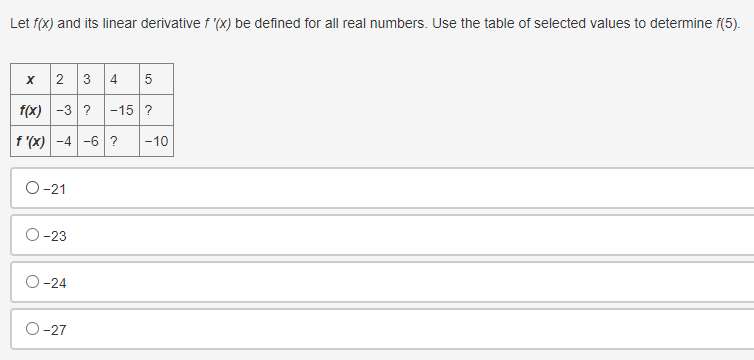
![direction between the given values, are shown in the table. FIX] 396](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667e115c856ad_012667e115c74230.jpg)

1)



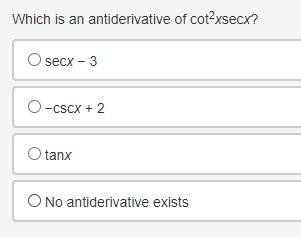

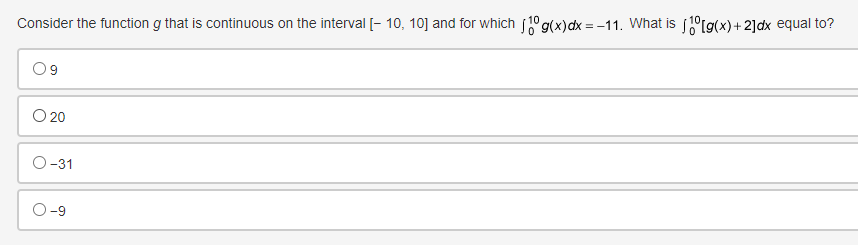
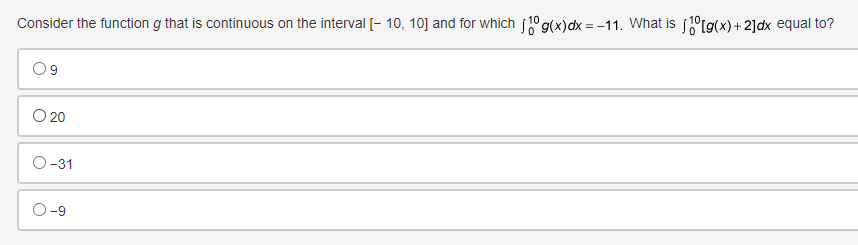
![on the interval [- 10, 10] and for which ]] g(x)dx =](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667e116127bf1_017667e11611297a.jpg)
![-11. What is /10[g(x) + 2]dx equal to? 09 O 20 O-31](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667e116174c4b_017667e116157133.jpg)
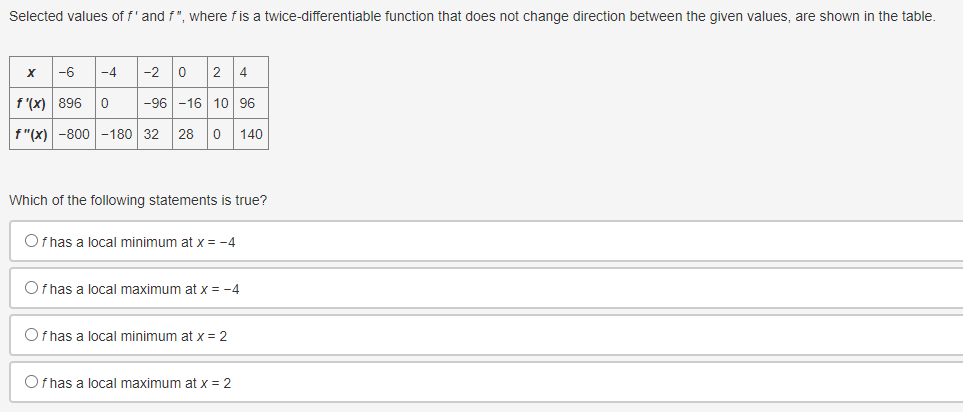
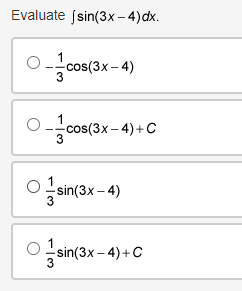
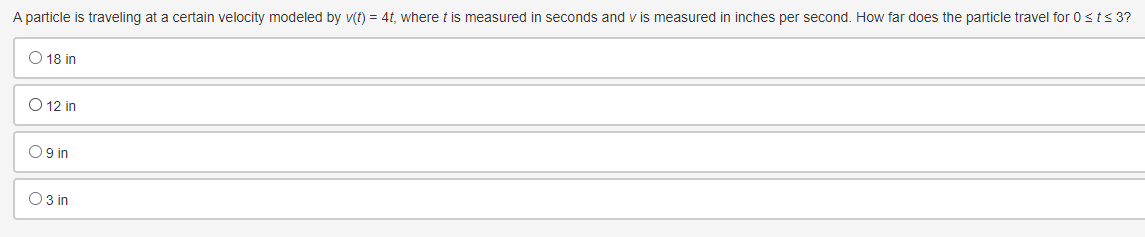
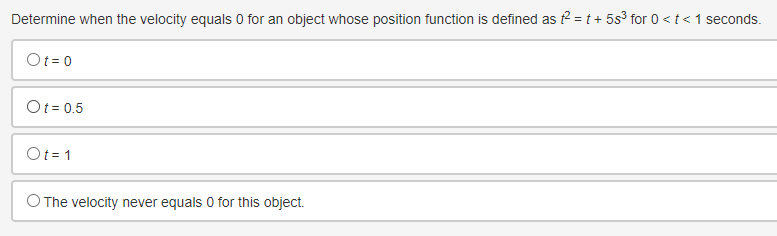
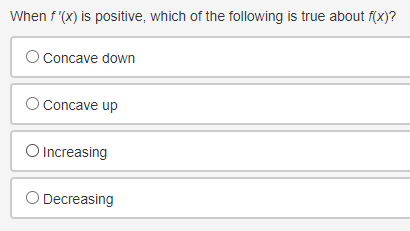
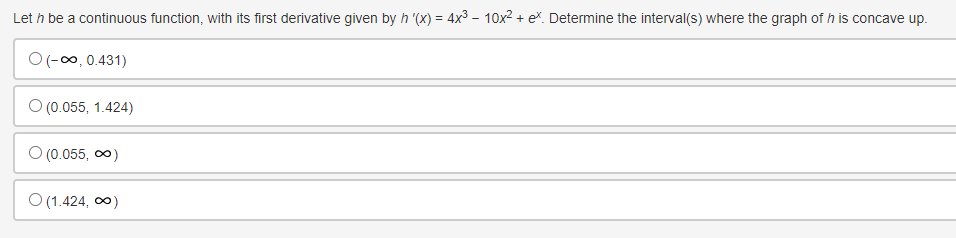
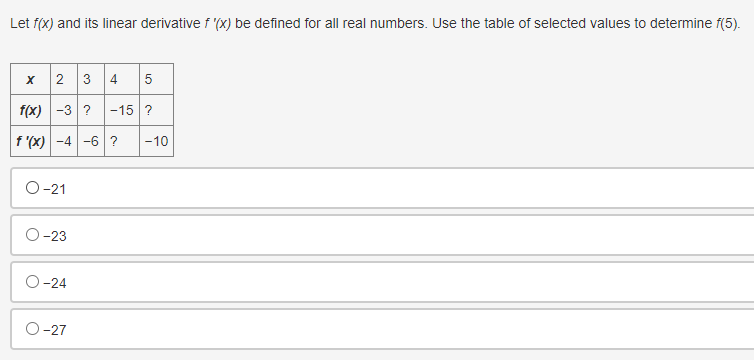
Use the trapezoidal rule to approximate fox dx, using three non-uniform partitions at {0, 0.25, 1.5, 2}. O (03 + 0.253)(1) + (0.253 + 1.53)(1) + (1.53 + 23)(1) O o.5[(03 + 0.253)(0.5) + (0.253 + 1.53)(0.5) + (1.53 + 23)(0.5)] O (03 + 0.253)(0.25) + (0.253 + 1.53)(1.25) + (1.53 + 23)(0.5) O 0.5[(03 + 0.253)(0.25) + (0.253 + 1.53)(1.25) + (1.53 + 23)(0.5)]Selected values of f ' and i' '1 where f is a Micedierentiable function that does not change direction between the given values, are shown in the table. FIX] 396 G 95 16 1G 95 Which of the following statements is true? \fEvaluate | sin(3x - 4) dx. O cos(3x - 4) O cos(3x - 4) + C O sin(3x - 4) O sin(3x -4) + CA particle is traveling at a certain velocity modeled by v(t) = 4t, where t is measured in seconds and v is measured in inches per second. How far does the particle travel for 0 s t s 3? O 18 in O 12 in 0 9 in 3 inDetermine when the velocity equals 0 for an object whose position function is defined as t- = t + 5s' for 0 0 for x > -2, then it can be concluded that fhas a relative minimum at x = -2. O True, the derivative changes from positive to negative O True, the derivative changes from negative to positive O False, the derivative changes from positive to negative O False, the derivative changes from negative to positiveConsider the function g that is continuous on the interval [- 10, 10] and for which ]] g(x)dx = -11. What is /10[g(x) + 2]dx equal to? 09 O 20 O-31 O-9Which of the following functions is guaranteed by the Extreme Value Theorem to have an absolute minimum on the interval [-10, 10]? f ( x ) = x g(x) = V2x Oh(x)= x-2 x- -4 Oj(x) = cosxA car travels east in a straight path at a speed of 80 miles per hour for 2 hours and then turns around and travels west in a straight path at a speed of 60 miles per hour for 2 hours. Taking direction into account, how many miles is the car from its starting position? O 40 miles 120 miles 160 miles O 280 miles
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


