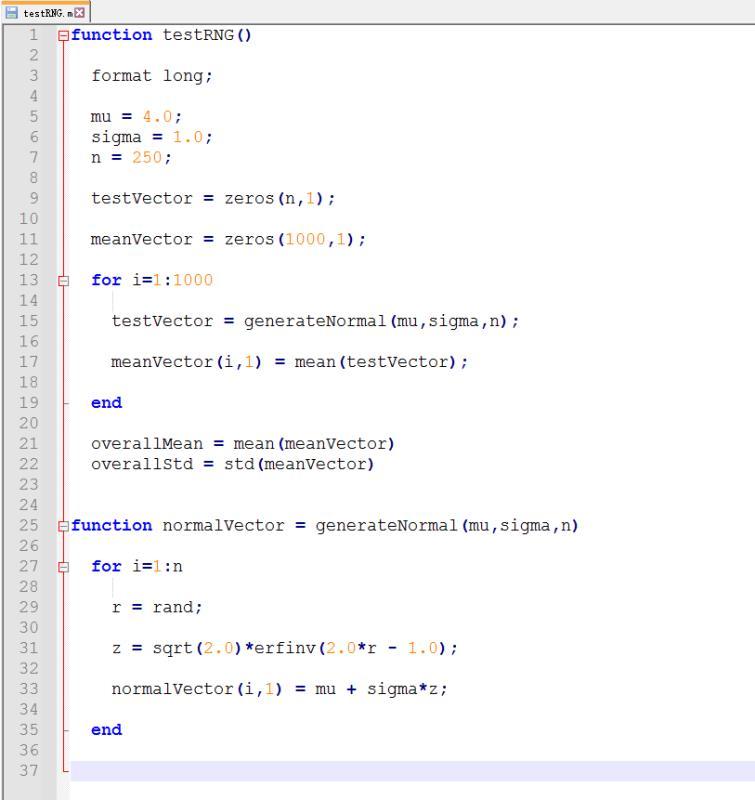
1. Using either the given C program testRNG.c, or the given Matlab program testRNG.m, test the hypothesis that the random number generator is biased; i.e., that the mean value of the means of repeated samples is not equal to the expected mean value of 4.0. Find the P-value of the test and state the conclusion. H:Hex = VS. H:l#H Generate 1000 samples of size 50, 100, 150, 200, and 250 to get observed mean values of the sample means. The expected mean value of the sample means for each value of n is 4.0. Sample Size (n) 200 50 100 150 250 Observed Mean of X's Expected Mean of X's 4.0 4.0 4.0 4.0 4.0 testRNG, X CO- OWN 1 function testRNG() 2 3 format long; 4 5 mu = 4.0; 6 sigma = 1.0; 7 n = 250; 9 testVector = zeros (n,1); 10 11 meanVector = zeros (1000,1); 12 13 for i=1:1000 14 15 testvector = generateNormal (mu, sigma, n) ; 16 17 meanVector (i,1) = mean (testVector); 18 end 19 20 21 22 overallMean = mean (meanVector) overallstd = std (meanVector) 23 24 25 function normalvector = generateNormal (mu, sigma,n) 26 27 for i=1:n 28 29 r = rand; 30 31 z = sqrt(2.0) *erfinv (2.0*r - 1.0); 32 33 normalVector(i, 1) = mu + sigma*z; 34 35 end 36 w . JO) 1 N 1. Using either the given C program testRNG.c, or the given Matlab program testRNG.m, test the hypothesis that the random number generator is biased; i.e., that the mean value of the means of repeated samples is not equal to the expected mean value of 4.0. Find the P-value of the test and state the conclusion. H:Hex = VS. H:l#H Generate 1000 samples of size 50, 100, 150, 200, and 250 to get observed mean values of the sample means. The expected mean value of the sample means for each value of n is 4.0. Sample Size (n) 200 50 100 150 250 Observed Mean of X's Expected Mean of X's 4.0 4.0 4.0 4.0 4.0 testRNG, X CO- OWN 1 function testRNG() 2 3 format long; 4 5 mu = 4.0; 6 sigma = 1.0; 7 n = 250; 9 testVector = zeros (n,1); 10 11 meanVector = zeros (1000,1); 12 13 for i=1:1000 14 15 testvector = generateNormal (mu, sigma, n) ; 16 17 meanVector (i,1) = mean (testVector); 18 end 19 20 21 22 overallMean = mean (meanVector) overallstd = std (meanVector) 23 24 25 function normalvector = generateNormal (mu, sigma,n) 26 27 for i=1:n 28 29 r = rand; 30 31 z = sqrt(2.0) *erfinv (2.0*r - 1.0); 32 33 normalVector(i, 1) = mu + sigma*z; 34 35 end 36 w . JO) 1 N