1: Using variable elimination (by hand!), compute the probability that a student who did well on the test actually understood the material, that is, compute P(+u| + e).  

2: For the above Bayesian network, label the following statements about conditional independence as true or false. 

For this question, you should consider only the structure of the Bayesian network, not the specific probabilities.

Explain each of your answers.

1. T and U are independent.

2. T and U are conditionally independent given I, E, and H.

3. T and U are conditionally independent given I and H.

4. E and H are conditionally independent given U.

5. E and H are conditionally independent given U, I, and T.

6. I and H are conditionally independent given E.

7. I and H are conditionally independent given T.

8. T and H are independent.

9. T and H are conditionally independent given E.

10. T and H are conditionally independent given E and U.

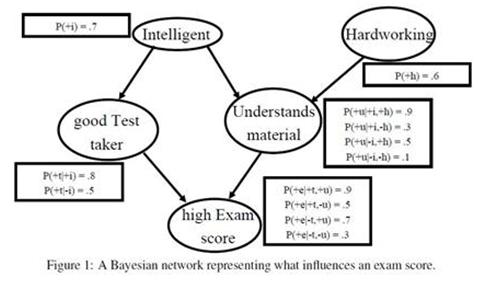
P(+1) -.7 Intelligent Hardworking P(+h) = .6 Understands P(+u+i-h) -9 P(+uti.-h) -3 P(+u-i+h) -5 P(+u-i-h) -.1 good Test material taker P(+t+1) = 8 P(+r-1) -.5 P(+e+t,+u) -9 P(+e+t.-u) -5 high Exam P(+e-t.+u) -.7 P(+el-1.-u) -3 score Figure 1: A Bayesian network representing what influences an exam score.