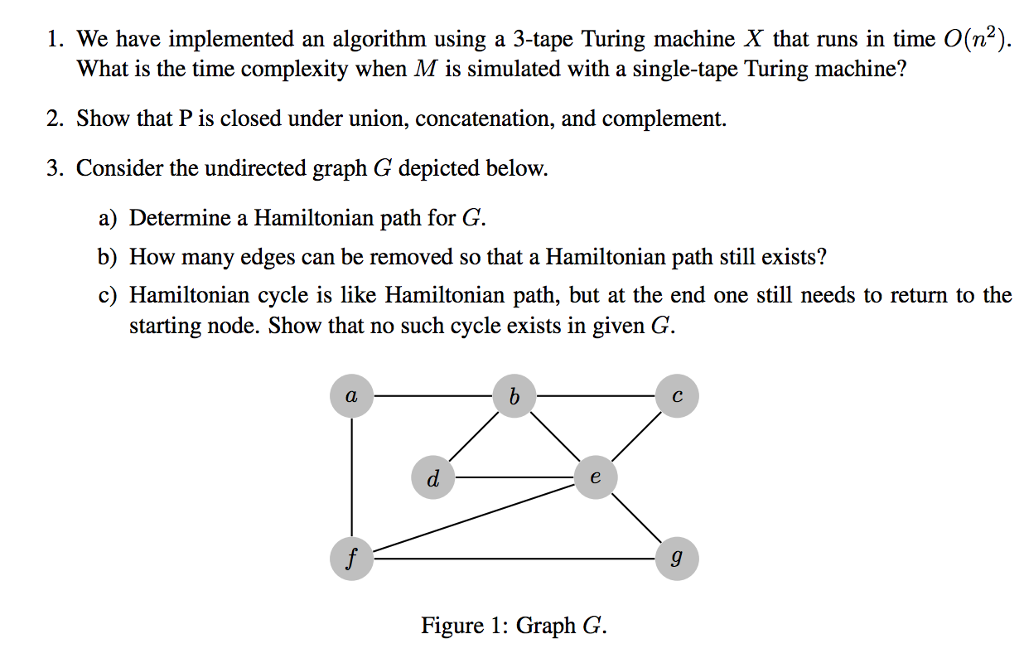
1. We have implemented an algorithm using a 3-tape Turing machine X that runs in time O(n2). What is the time complexity when M is simulated with a single-tape Turing machine? 2. Show that P is closed under union, concatenation, and complement 3. Consider the undirected graph G depicted below a) Determine a Hamiltonian path for G. b) How many edges can be removed so that a Hamiltonian path still exists? c) Hamiltonian cycle is like Hamiltonian path, but at the end one still needs to return to the starting node. Show that no such cycle exists in given G. Figure 1: Graph G 1. We have implemented an algorithm using a 3-tape Turing machine X that runs in time O(n2). What is the time complexity when M is simulated with a single-tape Turing machine? 2. Show that P is closed under union, concatenation, and complement 3. Consider the undirected graph G depicted below a) Determine a Hamiltonian path for G. b) How many edges can be removed so that a Hamiltonian path still exists? c) Hamiltonian cycle is like Hamiltonian path, but at the end one still needs to return to the starting node. Show that no such cycle exists in given G. Figure 1: Graph G