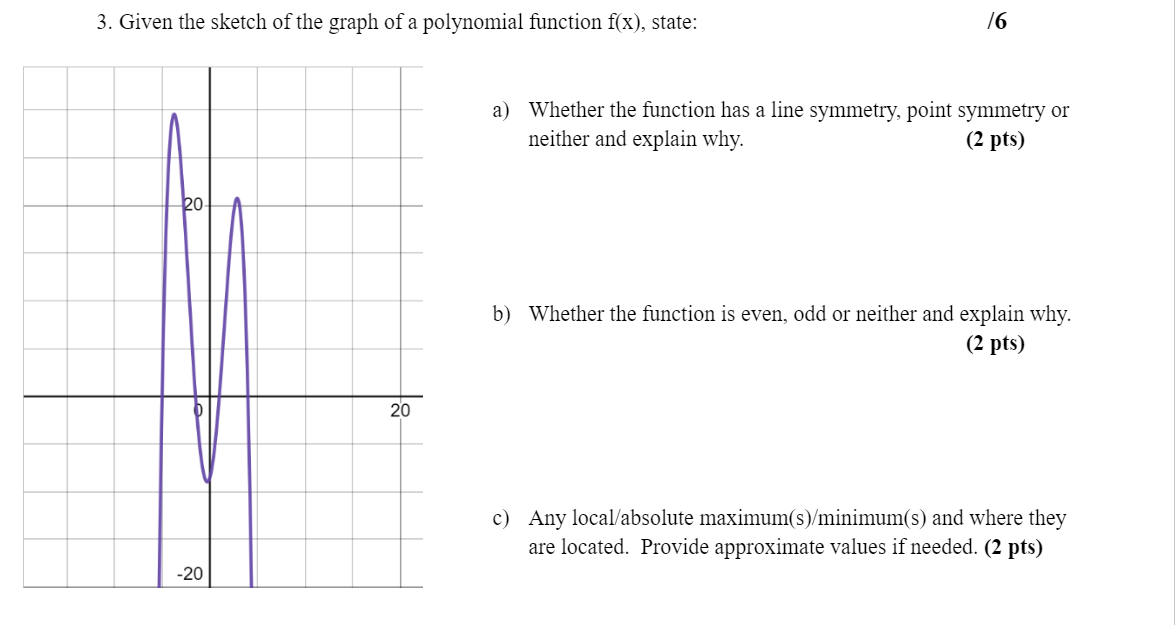
1. Without expanding, state the degree, the leading coefficient, and the end behaviours of the polynomial function g(x) = 2(x + 1)(3 - x) (x - 5). Provide a "sketch" of the function. Show all steps for full marks. 15 Degree (1 pt) Leading Coefficient (1 pt) End behaviours (1 pt) Y-intercept (1 pt) Sketch (1 pt)2. Write the equation and then sketch, :1 quartic polynomial function with zeros at -2. 3 (order 3). if f(0) = 18. f3 3. Given the sketch of the graph of a polynomial function f( x), state: f6 b) Whether the function has a line symmetry, point symmetry or neither and explain why. (2 pts) Whether the function is even, odd or neither and explain why. (2 PM Any local/absolute maximum(s)/minimum(s) and where they are located. Provide approximate values if needed. (2 pts) \f5. The table of values represents a polynomial function f (x). Use finite differences to determine the following: 18 X f (x) -3 -45 - 2 -16 - 1 -3 0 0 1 2 0 3 9 4 32m b) d} the degree 'n' of the polynomial function f (x) the Sign of the leading coefficient the value of the leading coefficient. an Find the polynomial function. (2 INS) (1 Pt) (2 INS) (3 pts)