1)

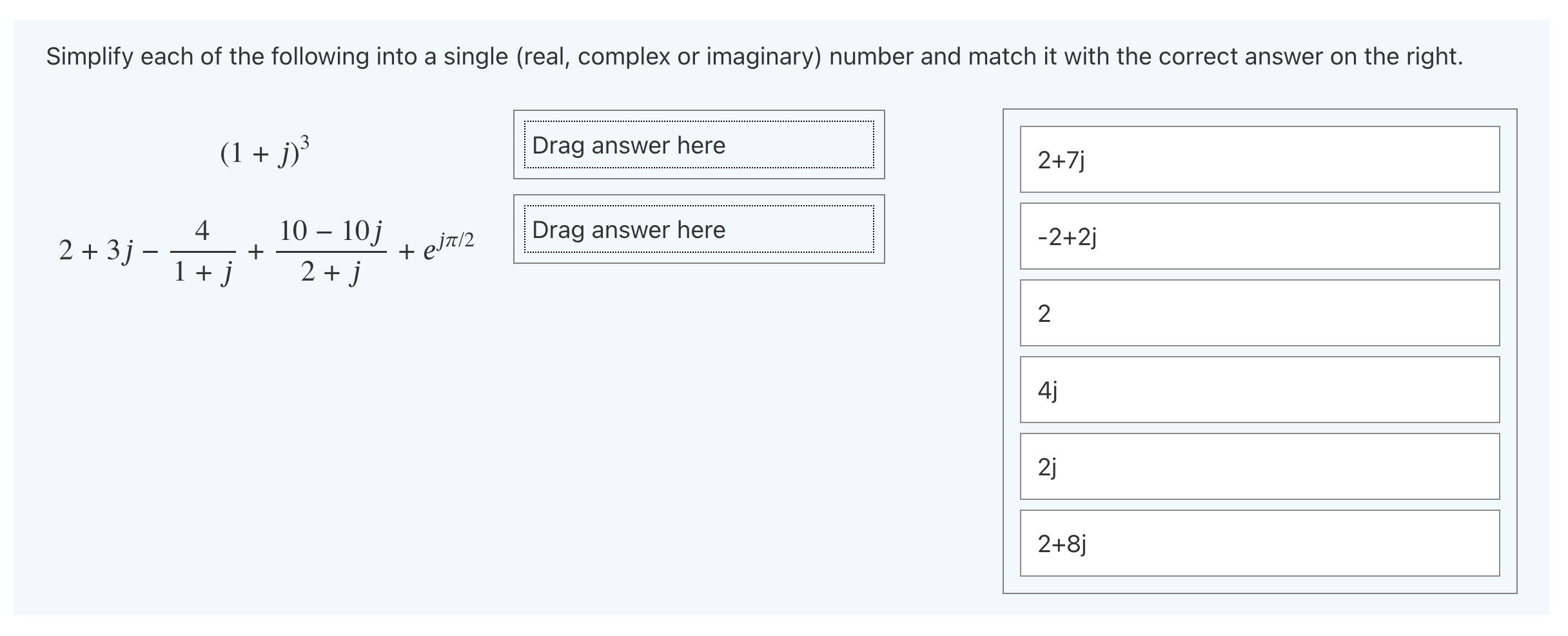
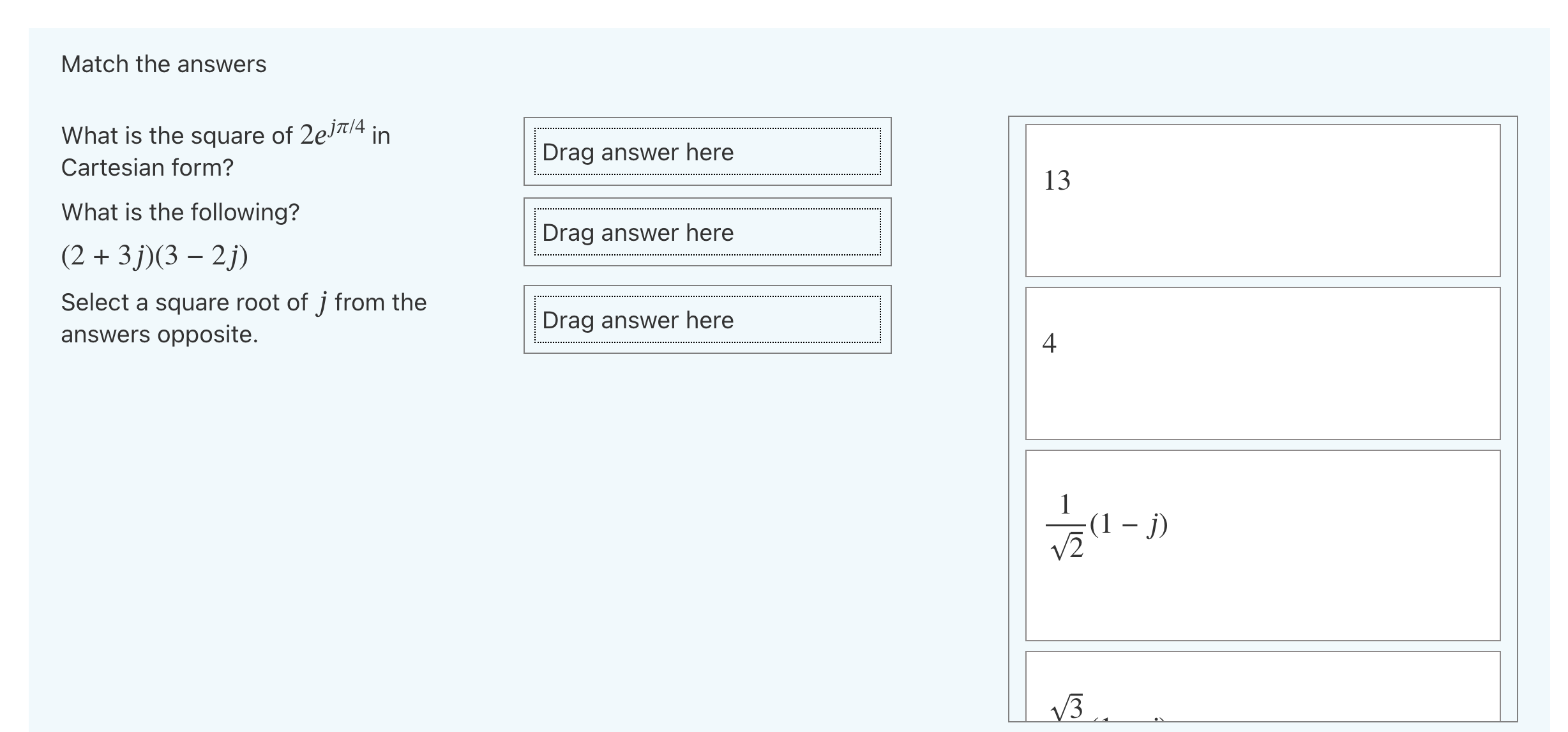
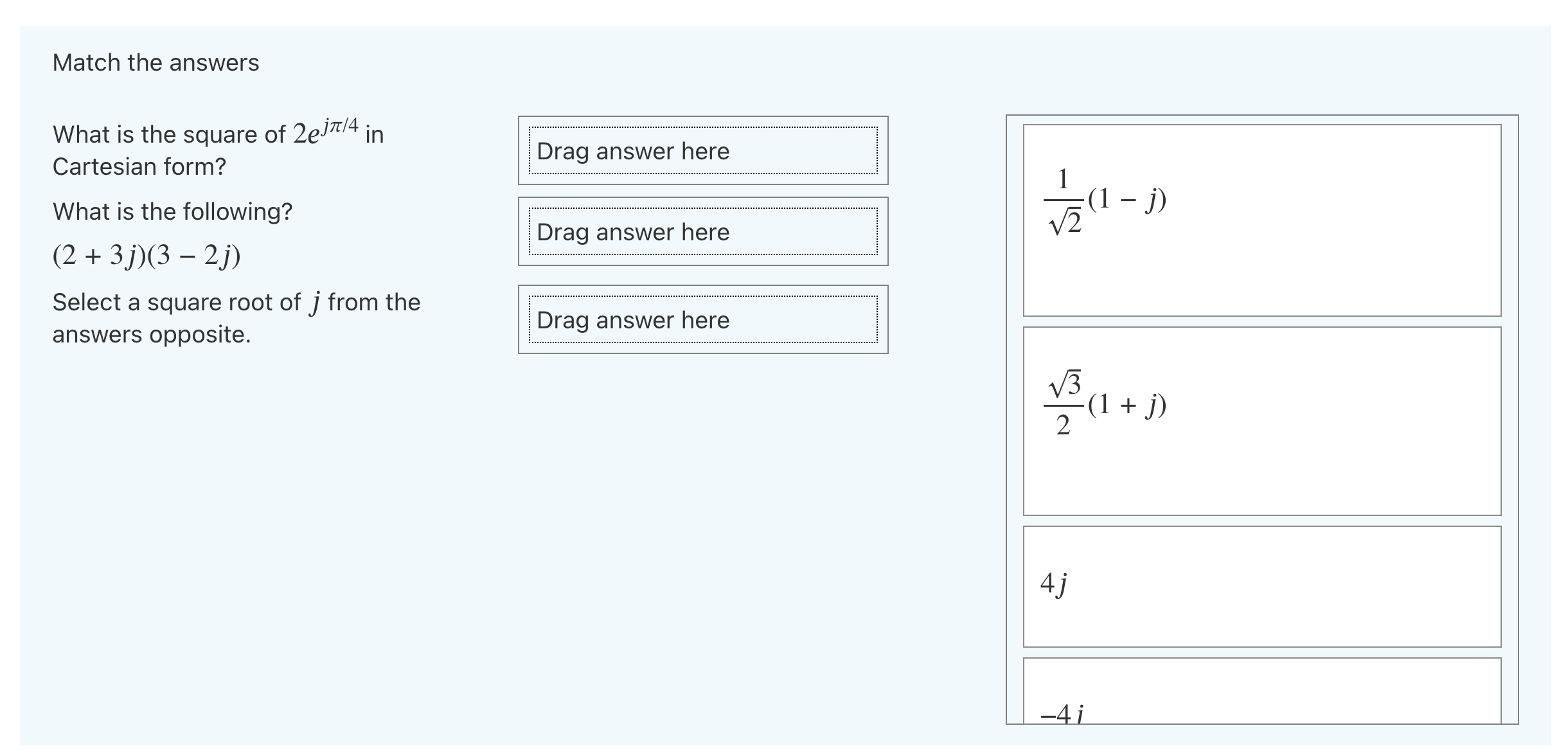
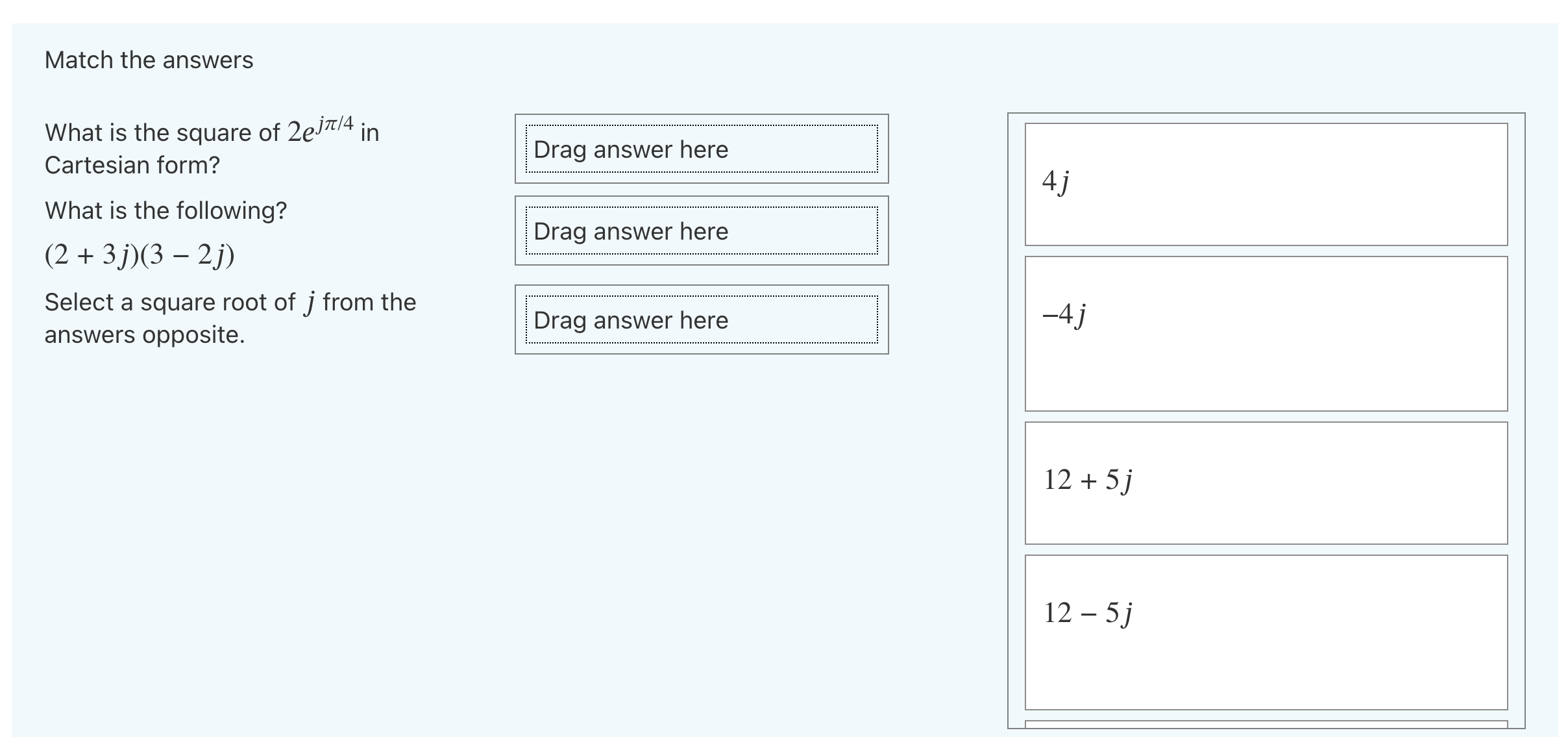
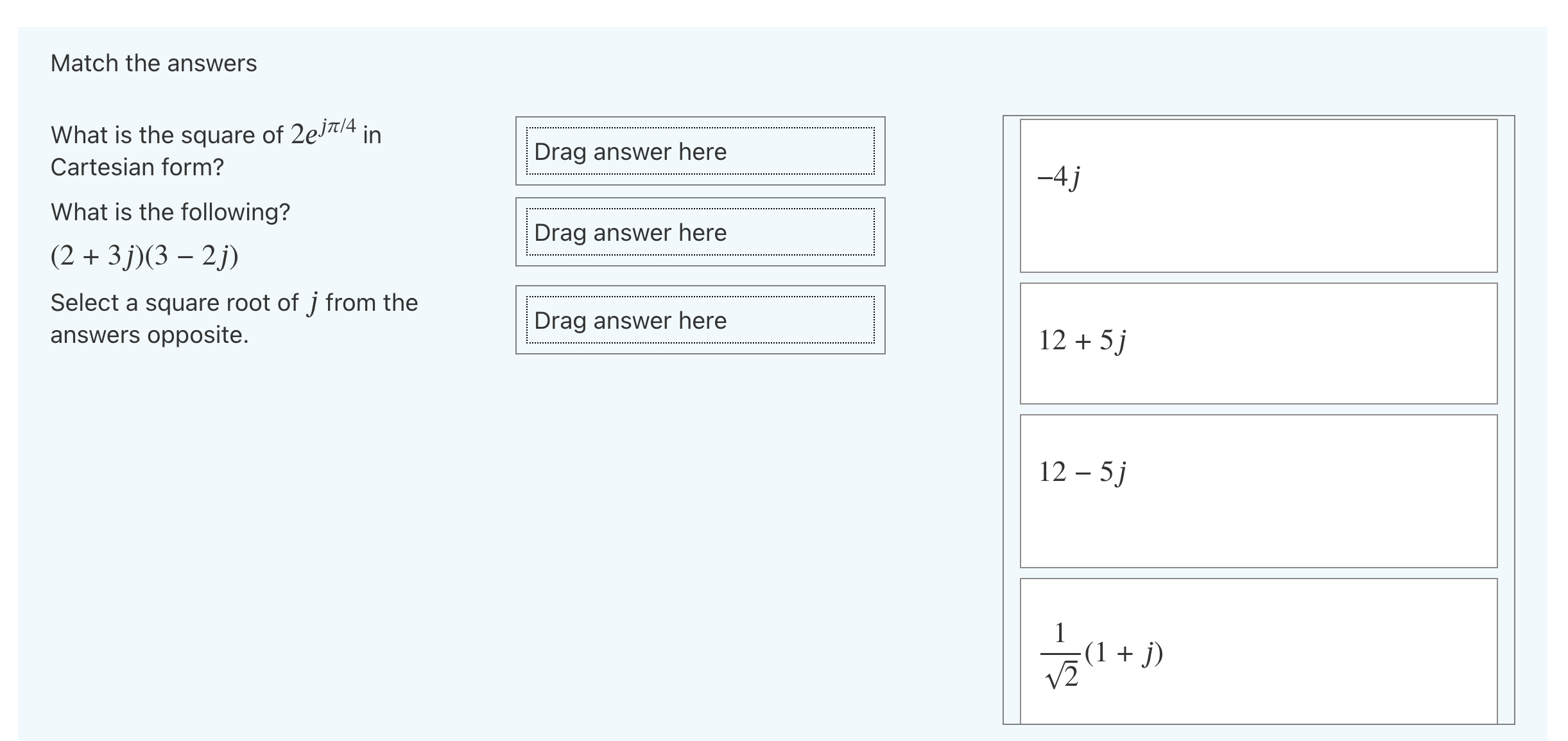
Write the complex number Z = 1+ V3j in polar form and raise it to the power of 4. If you think z4 = pelta type p in the box. Hint: there are very few complex numbers in polar form that are easy to write in the form a + jb. It must be related to one of them. Answer:Simplify each of the following into a single (real, complex or imaginary) number and match it with the correct answer on the right. rag answer here (1 + D3 2+7j -2+2j 4 1010] +ej7r/2 rag answer here 2+3j 1+j 2+j Match the answers What is the square of 2ej7T/4 in Cartesian form? What is the following? (2 + 3j)(3 - 2]) Select a square root of j from the answers opposite. Drag answer here Drag answer here 13 Drag answer here 5 Match the answers What is the square of 2ej'r/4 in Cartesian form? What is the following? (2 + 3])(3 - 2}) Select a square root of j from the answers opposite. rag answer here rag answer here rag answer here L 1_. ( J) Match the answers What is the square of 2ej7r/4 in Cartesian form? rag answer here What is the following? rag answer here (2 + 3])(3 - 21) Select a square root of j from the answers opposite. rag answer here '4] 12+$ 123 Match the answers What is the square of ZeW4 in Cartesian form? What is the following? (2 + 3j)(3 - 21') Select a square root of j from the answers opposite. rag answer here rag answer here rag answer here 12+5j 125j (1 +1)