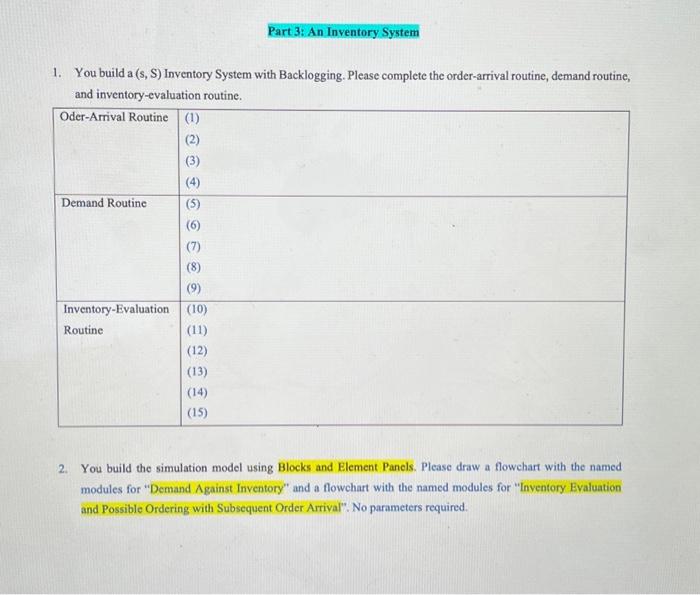
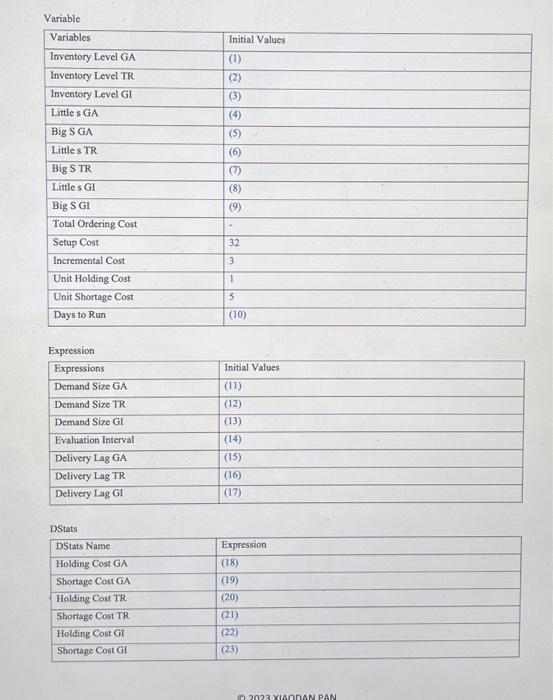
1. You build a (s,S) Inventory System with Backlogging. Please complete the order-arrival routine, demand routine, and inventorv-evaluation mutine 2. You build the simulation model using Blocks and Element Panels. Please draw a flowchart with the named modules for "Demand Against Inventory" and a flowehart with the named modules for "Inventory Evaluation and Possible Ordering with Subsequent Order Arrival". No parameters required. 3. With the knowledge of the (s, S) Inventory System, you are tasked with developing a simulation model of an inventory system for a retail store that sells THREE types of products: 1) gadgets (GA), 2) trinkets (TR), and 3) gizmos (GI). The store has an initial inventory of 60 gadgets, 50 trinkets, and 70 gizmos. The demand for gadgets is one, two, three, or four with respective probabilities 0.167,0.333,0.333, and 0.167 , respectively. The demand for trinkets and gizmos follows a Poisson distribution with means of 1.9 and 2.3 , respectively, and is independent of the demand for gadgets. The inventory system has one evaluator who arrives at the beginning of each day to assess the inventory levels and decide on orders. The evaluator must consider each inventory separately and order according to (s,S) policies, where s is the reorder point and S is the order-up-to level. For gadgets, (s,S)=(20, 40); for trinkets, (s,S)=(15,35); and for gizmos, (s,S)=(25,45). The delivery lags for gadgets, trinkets, and gizmos follow a uniform distribution with ranges of (0.5,1.0),(0.4,0.8), and (0.8,1.7), respectively. The ordering costs, holding costs, and shortage costs for trinkets and gizmos are the same as those for gadgets. Your task is to develop a simulation flowchart using Blocks and Element Panels to model this inventory system and run it for 360 days. The simulation should provide total daily costs, as well as separate holding and shortage costs for each type of product. Please draw a flowchart with the named modules for "Demand Against Inventory" and a flowchart with the named modules for "Inventory Evaluation and Possible Ordering with Subsequent Order Arrival" No parameters required. And then fill out modules from the element panel. Variable \begin{tabular}{|l|l|} \hline Variables & Initial Values \\ \hline Inventory Level GA & (1) \\ \hline Inventory Level TR & (2) \\ \hline Inventory Level GI & (3) \\ \hline Little s GA & (4) \\ \hline Big S GA & (5) \\ \hline Little S TR & (6) \\ \hline Big S TR & (7) \\ \hline Little s GI & (8) \\ \hline Big S GI & (9) \\ \hline Total Ordering Cost & - \\ \hline Setup Cost & 32 \\ \hline Incremental Cost & 3 \\ \hline Unit Holding Cost & 1 \\ \hline Unit Shortage Cost & 5 \\ \hline Days to Run & (10) \\ \hline \end{tabular} Expression \begin{tabular}{|l|l|} \hline Expressions & Initial Values \\ \hline Demand Size GA & (11) \\ \hline Demand Size TR & (12) \\ \hline Demand Size GI & (13) \\ \hline Evaluation Interval & (14) \\ \hline Delivery Lag GA & (15) \\ \hline Delivery Lag TR & (16) \\ \hline Delivery Lag GI & (17) \\ \hline \end{tabular} DStats \begin{tabular}{|l|l|} \hline DStats Name & Expression \\ \hline Holding Cost GA & (18) \\ \hline Shortage Cost GA & (19) \\ \hline Holding Cost TR & (20) \\ \hline Shortage Cost TR & (21) \\ \hline Holding Cost GI & (22) \\ \hline Shortage Cost GI & (23) \\ \hline \end{tabular} 1. You build a (s,S) Inventory System with Backlogging. Please complete the order-arrival routine, demand routine, and inventorv-evaluation mutine 2. You build the simulation model using Blocks and Element Panels. Please draw a flowchart with the named modules for "Demand Against Inventory" and a flowehart with the named modules for "Inventory Evaluation and Possible Ordering with Subsequent Order Arrival". No parameters required. 3. With the knowledge of the (s, S) Inventory System, you are tasked with developing a simulation model of an inventory system for a retail store that sells THREE types of products: 1) gadgets (GA), 2) trinkets (TR), and 3) gizmos (GI). The store has an initial inventory of 60 gadgets, 50 trinkets, and 70 gizmos. The demand for gadgets is one, two, three, or four with respective probabilities 0.167,0.333,0.333, and 0.167 , respectively. The demand for trinkets and gizmos follows a Poisson distribution with means of 1.9 and 2.3 , respectively, and is independent of the demand for gadgets. The inventory system has one evaluator who arrives at the beginning of each day to assess the inventory levels and decide on orders. The evaluator must consider each inventory separately and order according to (s,S) policies, where s is the reorder point and S is the order-up-to level. For gadgets, (s,S)=(20, 40); for trinkets, (s,S)=(15,35); and for gizmos, (s,S)=(25,45). The delivery lags for gadgets, trinkets, and gizmos follow a uniform distribution with ranges of (0.5,1.0),(0.4,0.8), and (0.8,1.7), respectively. The ordering costs, holding costs, and shortage costs for trinkets and gizmos are the same as those for gadgets. Your task is to develop a simulation flowchart using Blocks and Element Panels to model this inventory system and run it for 360 days. The simulation should provide total daily costs, as well as separate holding and shortage costs for each type of product. Please draw a flowchart with the named modules for "Demand Against Inventory" and a flowchart with the named modules for "Inventory Evaluation and Possible Ordering with Subsequent Order Arrival" No parameters required. And then fill out modules from the element panel. Variable \begin{tabular}{|l|l|} \hline Variables & Initial Values \\ \hline Inventory Level GA & (1) \\ \hline Inventory Level TR & (2) \\ \hline Inventory Level GI & (3) \\ \hline Little s GA & (4) \\ \hline Big S GA & (5) \\ \hline Little S TR & (6) \\ \hline Big S TR & (7) \\ \hline Little s GI & (8) \\ \hline Big S GI & (9) \\ \hline Total Ordering Cost & - \\ \hline Setup Cost & 32 \\ \hline Incremental Cost & 3 \\ \hline Unit Holding Cost & 1 \\ \hline Unit Shortage Cost & 5 \\ \hline Days to Run & (10) \\ \hline \end{tabular} Expression \begin{tabular}{|l|l|} \hline Expressions & Initial Values \\ \hline Demand Size GA & (11) \\ \hline Demand Size TR & (12) \\ \hline Demand Size GI & (13) \\ \hline Evaluation Interval & (14) \\ \hline Delivery Lag GA & (15) \\ \hline Delivery Lag TR & (16) \\ \hline Delivery Lag GI & (17) \\ \hline \end{tabular} DStats \begin{tabular}{|l|l|} \hline DStats Name & Expression \\ \hline Holding Cost GA & (18) \\ \hline Shortage Cost GA & (19) \\ \hline Holding Cost TR & (20) \\ \hline Shortage Cost TR & (21) \\ \hline Holding Cost GI & (22) \\ \hline Shortage Cost GI & (23) \\ \hline \end{tabular}