Question: 1. You draw one card randomly from a standard deck of 52 playing cards (no jokers) Event A: You draw a heart card. Event B:

1. You draw one card randomly from a standard deck of 52 playing cards (no jokers)

Event A: You draw a heart card.

Event B: You draw a card that is not a face card.

Event C: You draw a non-face card that is divisible by 3.

What is the probability that Event A, B, or C will occur?

2. Empirically verify the probability you calculated in Problem 1 with a Python program that simulates drawing randomly from a deck of cards. Initialize a list of cards, each card with a suit and a value. Generate a random number 0 through 51 to pick a card from the list. Check for Events A, B, and C. Repeat this a million times and count how many times Event A, B, or C occurred. After a million card picks, print your count divided by a million. How well does this simulation probability match the probability you calculated in Problem 9? Also print the simulation probabilities after 100; 1,000; 10,000; and 100,000 card picks. Determine how many simulated card picks are needed for the simulation probability to match your calculated probability to 3 decimal places.

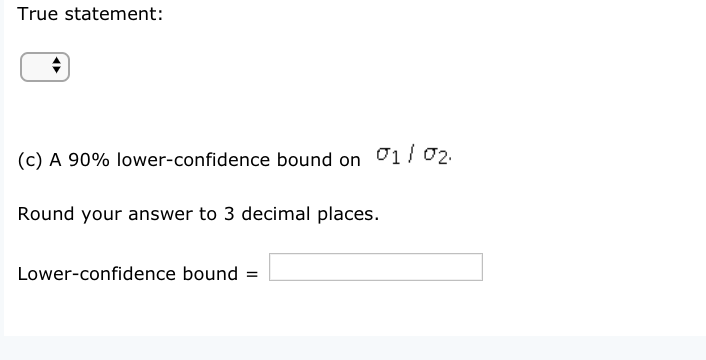
1. You draw one card randomly from a standard deck of 52

playing cards (no jokers) Event A: You draw a heart card.Event B:

True statement: (c) A 90% lower-confidence bound on 1 / 02. Round your answer to 3 decimal places. Lower-confidence bound =Compute the theoretical mean of the random variable X for the given probability distribution. My -(Round to three decimal places as needed.) 1,673 Compute the theoretical standard deviation of the random variable X for the given probability distribution 6, -(Round to three decimal places as needed.) 1.23| Approximate the mean of the random variable X based on the simulation for 25 games. x =(Round to three decimal places as needed.) Approximate the standard deviation of the random variable X based on the simulation for 25 games. s-(Round to three decimal places as needed.) Approximate the mean of the random variable X based on the simulation for 50 games. x =(Round to three decimal places as needed.) Approximate the standard deviation of the random variable X based on the simulation for 50 games. s-(Round to three decimal places as needed.) What property is being illustrated? Chebyshev's inequality The Law of Large Numbers O The empirical rule

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1. You draw one card randomly from a standard deck of 52 playing cards (no jokers) Event A: You draw a heart card. Event B: You draw a card that is not a face card. Event C: You draw a non-face card...

Problem 1 : Simulating Blackjack In this problem we will use classes and functions to simulate a simplified game of Blackjack ( 2 1 ) . The game begins with a standard deck of 5 2 playing cards ( no...

Give a detailed work please thankyou 7. Knowledge of economics is divided into 3 groups: 20% of the population is Excellent, 60% Good, and 20% Weak. Past studies have found that 70% of those in the...

* * * HELP in JAVA * * * I feel like I ' m so close to getting it to work but I don't know what to do with my objects to make it effective:Write a BlackJack program that plays a game of BlackJack....

probability and statistics: 1. Select the events that are mutually exclusive. a) Rolling a sum of 2 or rolling a prime number with a pair of six-sided dice, numbered 1 to 6. b) Rolling a sum of 6 or...

U E S T I O N 1 Provide an appropriate response. A card is drawn from a standard deck of 52 playing cards. Find the probability that the card is an ace or a heart. A. 7/52 B 17/52 C 3/13 D 4/13 Q U E...

In a standard deck of 52 playing cards, each card is one of the following kinds : Ace (A), 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack (J), Queen (Q), and King (K). In the card game Poker, you can think of the...

In a standard deck of 52 playing cards, each card is one of the following kinds: Ace (A), 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack (J), Queen (Q), and King (K). In the card game Poker, you can think of the...

(solve in java only)In a standard deck of 52 playing cards, each card is one of the following kinds: Ace (A), 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack (J), Queen (Q), and King (K). In the card game Poker,...

Southern Atlantic Distributors began operations in January 2018 and purchased a delivery truck for $40,000. Southern Atlantic plans to use straight-line depreciation over a four-year expected useful...

You are planning to acquire an asset for use in your business. In groups of three or four, use the Internet to research some factors that should be considered in deciding whether to purchase or lease...

The cost formula for a company can be modeled by C 66050x03x2 where x represents the number of items made A formula for the companys income is modeled with R10where is the number of items sold A...

A project that costs $200 million is expected to produce $80 million in year 1, $100 million in year 2, and $90 million in year 3. The project's cost of capital is 4%. 1) Find the payback period. 2)...

2. One union newspaper indicated how it saved an employees job. The employee was in the mechanics classification and was discharged for refusing to comply with managements sudden, unilateral rule...

broadening cross-cultural analysis to include an understanding of integrationdifferentiation in global managing;

developing the relevance of cross-cultural studies through an incorporation of stakeholder analysis of particular interaction situations;