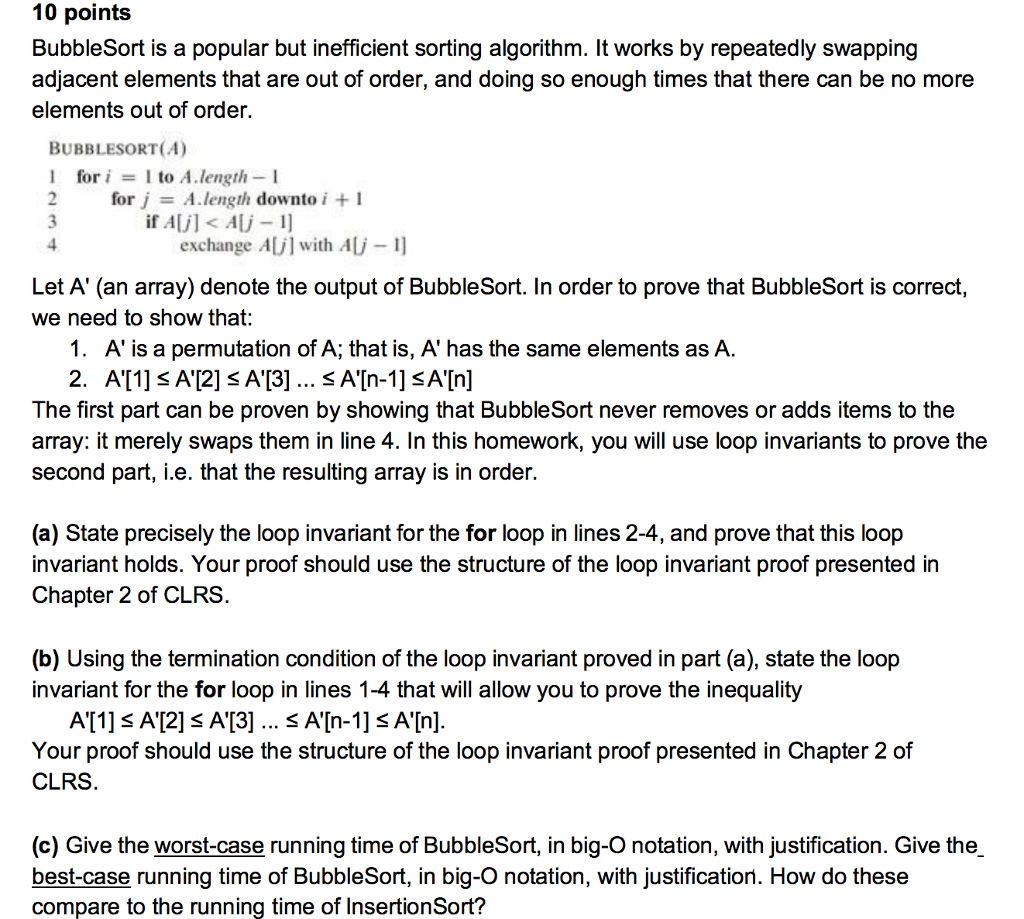
10 points BubbleSort is a popular but inefficient sorting algorithm. It works by repeatedly swapping adjacent elements that are out of order, and doing so enough times that there can be no more elements out of order. BUBBLESORT(A) l fori to A.length -1 for j A . length downto i + 1 exchange Ajl with ALi -I] Let A' (an array) denote the output of BubbleSort. In order to prove that BubbleSort is correct, we need to show that: 1. A' is a permutation of A; that is, A' has the same elements as A The first part can be proven by showing that BubbleSort never removes or adds items to the array: it merely swaps them in line 4. In this homework, you will use loop invariants to prove the second part, i.e. that the resulting array is in order. (a) State precisely the loop invariant for the for loop in lines 2-4, and prove that this loop invariant holds. Your proof should use the structure of the loop invariant proof presented in Chapter 2 of CLRS (b) Using the termination condition of the loop invariant proved in part (a), state the loop invariant for the for loop in lines 1-4 that will allow you to prove the inequality Your proof should use the structure of the loop invariant proof presented in Chapter 2 of CLRS. (c) Give the worst-case running time of BubbleSort, in big-O notation, with justification. Give the best-case running time of BubbleSort, in big-O notation, with justification. How do these compare to the running time of InsertionSort