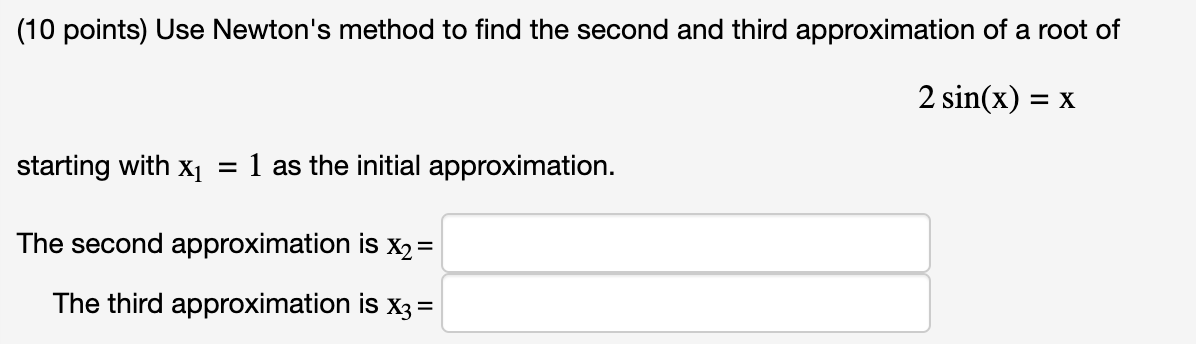
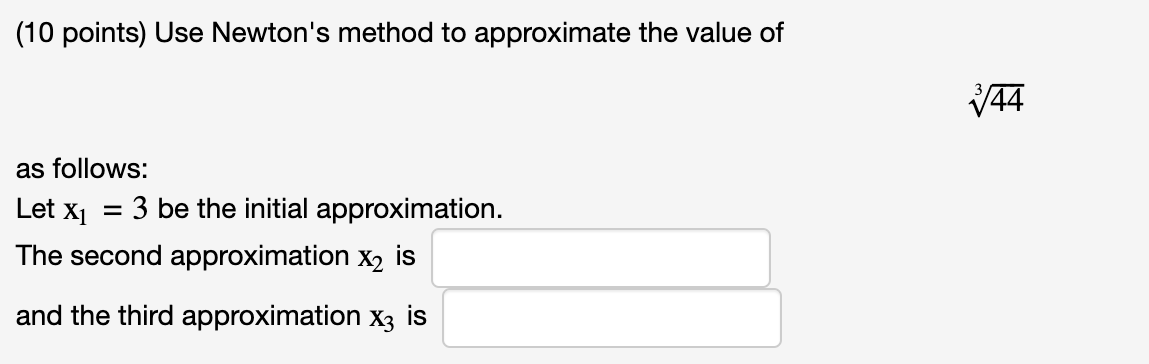
(10 points) Use Newton's method to find the second and third approximation of a root of starting with X1 = 1 as the initial approximation. The second approximation is x2 = The third approximation is x3 = 2 sin(x) = x (10 points) Use Newton's method to find the second and third approximation of a root of starting with X = -1 as the initial approximation. The second approximation is 2= The third approximation is x3 = x3 + x + 2 = 0 (10 points) Use Newton's method to approximate the value of as follows: Let X1 = The second approximation X2 is 3 be the initial approximation. and the third approximation X3 is /44 Use Newton's method to approximate the indicated root of the following equation correct to six decimal places. The root of x4 + x - 4 = 0 in the interval [1,2].