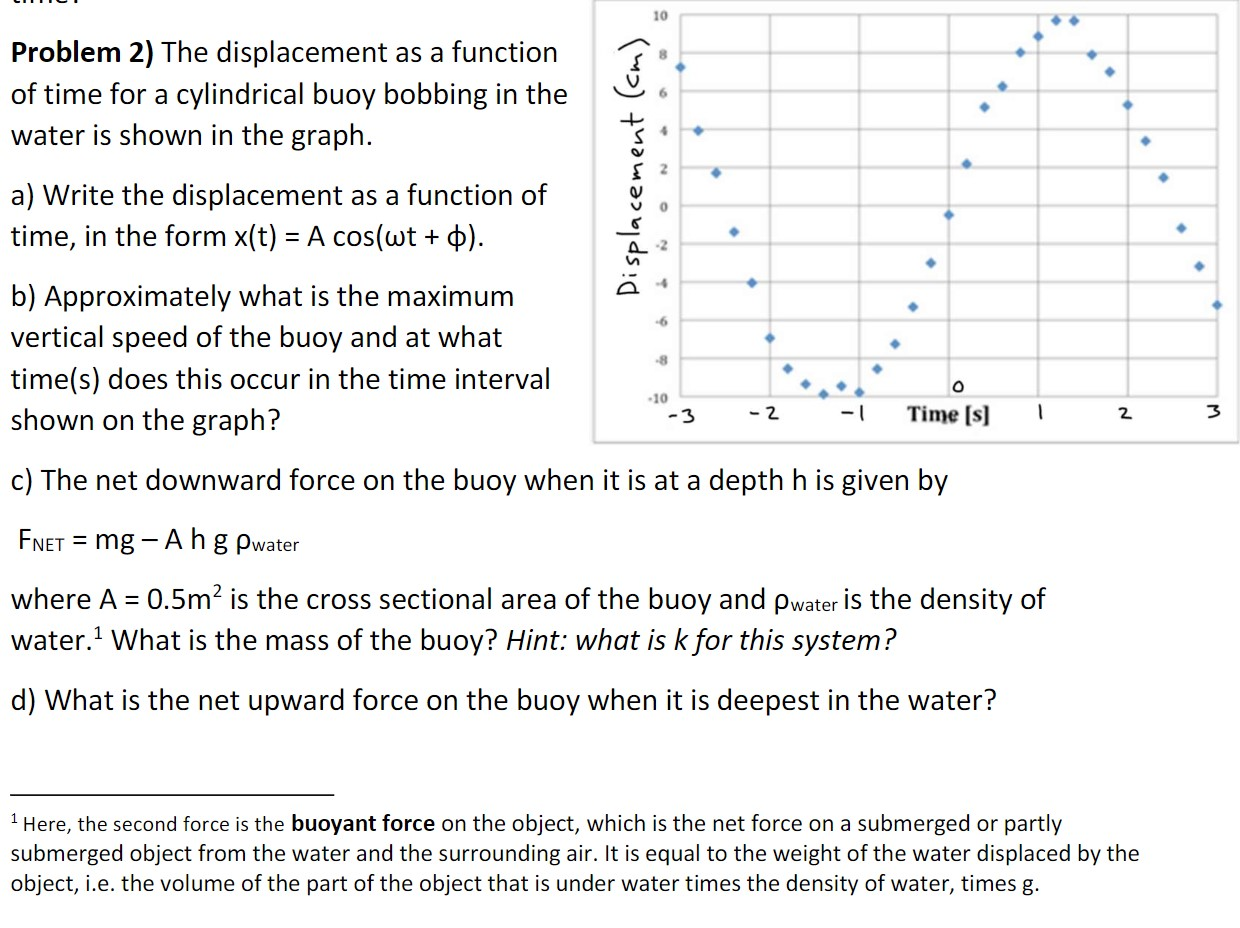
Problem 2) The displacement as a function of time for a cylindrical buoy bobbing in the water is shown in the graph. Displacement (cm) 10 8 6 -2 a) Write the displacement as a function of time, in the form x(t) = A cos(wt + p). b) Approximately what is the maximum vertical speed of the buoy and at what time(s) does this occur in the time interval shown on the graph? c) The net downward force on the buoy when it is at a depth h is given by FNET = mg - Ahg Pwater where A = 0.5m is the cross sectional area of the buoy and Pwater is the density of water. What is the mass of the buoy? Hint: what is k for this system? d) What is the net upward force on the buoy when it is deepest in the water? -4 -6 -8 -10 -3 -2 -1 O Time [s] 1 2 Here, the second force is the buoyant force on the object, which is the net force on a submerged or partly submerged object from the water and the surrounding air. It is equal to the weight of the water displaced by the object, i.e. the volume of the part of the object that is under water times the density of water, times g. 3