Question: (100 points) Let V = R2. For (u1, u2), (v1, U2) E V and a E R define vector addition by (uj, u2) (v1, U2)

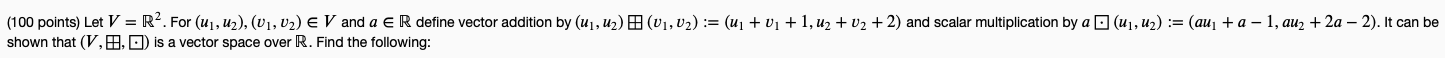
(100 points) Let V = R2. For (u1, u2), (v1, U2) E V and a E R define vector addition by (uj, u2) (v1, U2) := (uj + Uj + 1, uz + U2 + 2) and scalar multiplication by a [ (u1, u2) := (au + a - 1, au2 + 2a - 2). It can be shown that (V, #, [) is a vector space over R. Find the following:the sum: (9,9) : (-7,3) =( the scalar multiple: -50 (9,9) =( the zero vector: the additive inverse of (x, y): B(x, y) =(

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Section 3.1 Vector Spaces: Problem 6 (1 point) Let V = R2. For (u1, u2), (v1, v2) E V and a E IR define vector addition by (u1, (2) E (v1, V2) := (u1 + v1 - 3, u2 + v2 + 2) and scalar multiplication...

15. (10 pts) 1. Let V = R2, and define addition and scalar multiplication as follows: utv = (u1, U2) + (U1, U2) = (u101, u202) ku = k(u1, u2) = (up, u) Given that V is a vector space, (a) determine...

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

Let V = R. For u, v E V and a E R define vector addition by ull v := u + v - 1 and scalar multiplication by a Ju := au - a + 1. It can be shown that (V, , D) is a vector space over the scalar field...

Chapter 6.1 Write on paper for upvote. questions: 23, 25, 37, 41 please 10. U = [_3 31. =18 8] 27. a. (2v - w, 3u + 2w) b. llu + vil In Exercises 11-12, find the standard inner product on P2 of the...

(chapter 4.1) Questions: 1,2,3, 5, 8, 9 On paper please thanks a lot! Exercise Set 4.1 1. Let V be the set of all ordered pairs of real numbers, and con- d. Show that Axiom 5 holds by producing a...

Calculus 3 Sections 12.1 and 12.2 Reading Assignment: 3D Coordinates and Vectors Answer Only Exercise 1 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three...

- Symbolic functions must be entered using notation similar to the examples given below. - Do NOT include the name of the function or an equal sign. {i.e., do NOT include anything like '1' =' in your...

e OA11 (page 2 of 10) X Transition Matrix Calculator - Onl x G change of basis matrix calculator x Introducing ChatGPT x New chat x | + V X...

Grades: \\ X @ Safety Q X Circular ( X e OA11 (pa X G If T:R109 X Linear In X G (a) find t x Introduci X Linear trc X * Course H X New Tab X + V X...

Impacts on risk and term structures of interest rates from U.S. Treasury actions to borrow from markets, Impacts on long-term interest rates and yield curve from Feds policies to decrease inflation,...

Abraham Lincoln once said You can fool all of the people some of the time, and some of the people all of the time, but you cannot fool all of the people all of the time. How can a central bank that...

the yield on a 3 - year corporate bond should always exceed the yield on a 2 - year corporate bond

Can someone help me verify if these answers are correct Choices (5 Points) Mack has a basis in a partnership interest of $200,000, including his share of partnership debt. At the end of the current...