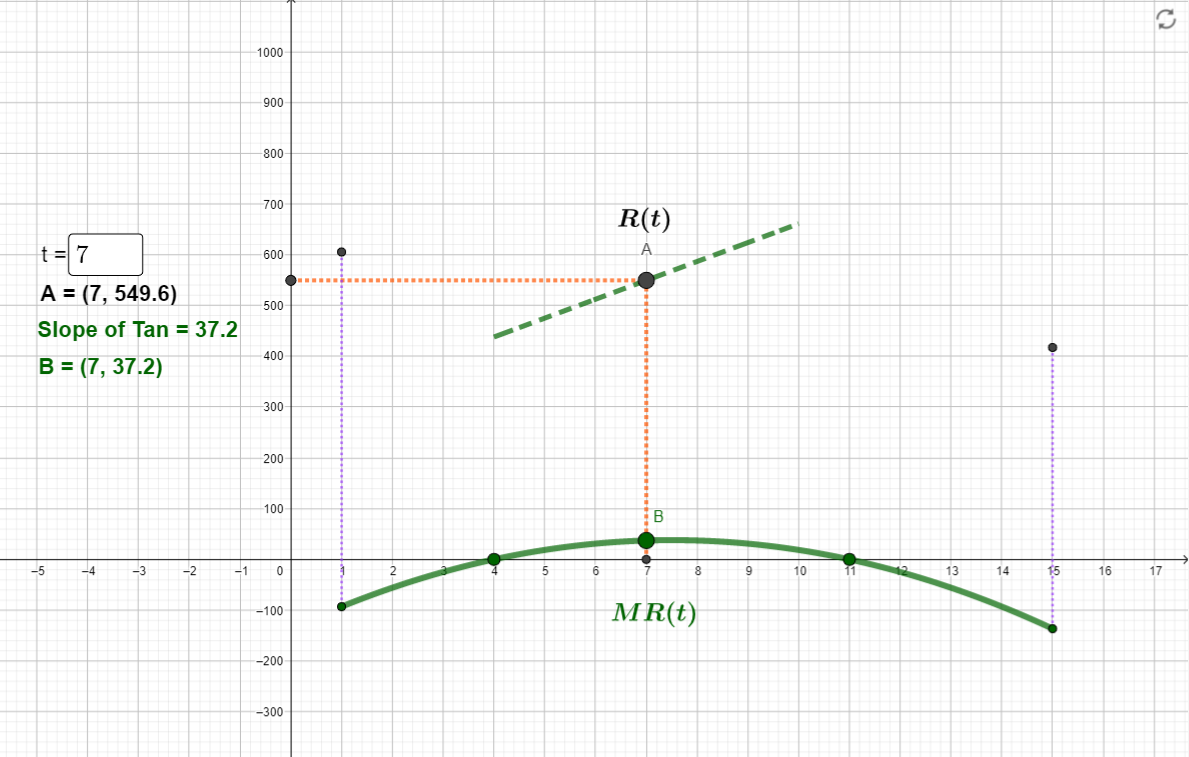
1000 900 800 700 R(t) 600 + = 7 A = (7, 549.6) Slope of Tan = 37.2 B = (7, 37.2) 500 . 400 300 200 100 B -5 -4 -3 -2 -1 0 5 6 8 9 10 11 19 13 14 15 16 17 -100 MR(t) -200 -300 Kruger Industrial Smoothing supplies hardware stores around the US with grinders, sanders, whetstones and other smoothing tools. Kruger's marginal revenue function, MR(t), gives the rate of change of revenue in hundreds of thousands of dollars per year, where t is the number of years since 2002. The graph of MR(t) is displayed in the applet above. Observe that as you drag point B along the marginal revenue curve, the point A traces out the graph of the revenue function, R(t). The tangent line to R(t) at point A is also provided. Use the above applet to answer the following questions. (a) According to the graph, the functions R(t) and MR(t) each have a domain of ( use interval notation ). Thus, Kruger's revenue model is valid from year to year (b) The year 2006 corresponds to an input of t = In 2006, Kruger had a total revenue of hundred thousand dollars and in that year the revenue was ??? at a rate of hundred thousand dollars per year. (c) The critical values of R(t) are (list critical values, separated by a comma). These critical values correspond to the years and ( list years in order). Kruger's marginal revenue was negative from t = (d) Kruger's marginal revenue was positive from t = to t= to t= and then was negative again from t = to t= and . Kruger's revenue was decreasing from (e) Kruger's revenue was increasing between the years to and then was decreasing again between and when the company's total revenue was hundred thousand (f) Kruger's revenue was at a relative maximum in the year dollars. In that year, Kruger's marginal revenue was hundred thousand dollars per year. when the company's total revenue was hundred thousand (9) Kruger's revenue was at a relative minimum in the year dollars. In that year, Kruger's marginal revenue was hundred thousand dollars per year. 1000 900 800 700 R(t) 600 + = 7 A = (7, 549.6) Slope of Tan = 37.2 B = (7, 37.2) 500 . 400 300 200 100 B -5 -4 -3 -2 -1 0 5 6 8 9 10 11 19 13 14 15 16 17 -100 MR(t) -200 -300 Kruger Industrial Smoothing supplies hardware stores around the US with grinders, sanders, whetstones and other smoothing tools. Kruger's marginal revenue function, MR(t), gives the rate of change of revenue in hundreds of thousands of dollars per year, where t is the number of years since 2002. The graph of MR(t) is displayed in the applet above. Observe that as you drag point B along the marginal revenue curve, the point A traces out the graph of the revenue function, R(t). The tangent line to R(t) at point A is also provided. Use the above applet to answer the following questions. (a) According to the graph, the functions R(t) and MR(t) each have a domain of ( use interval notation ). Thus, Kruger's revenue model is valid from year to year (b) The year 2006 corresponds to an input of t = In 2006, Kruger had a total revenue of hundred thousand dollars and in that year the revenue was ??? at a rate of hundred thousand dollars per year. (c) The critical values of R(t) are (list critical values, separated by a comma). These critical values correspond to the years and ( list years in order). Kruger's marginal revenue was negative from t = (d) Kruger's marginal revenue was positive from t = to t= to t= and then was negative again from t = to t= and . Kruger's revenue was decreasing from (e) Kruger's revenue was increasing between the years to and then was decreasing again between and when the company's total revenue was hundred thousand (f) Kruger's revenue was at a relative maximum in the year dollars. In that year, Kruger's marginal revenue was hundred thousand dollars per year. when the company's total revenue was hundred thousand (9) Kruger's revenue was at a relative minimum in the year dollars. In that year, Kruger's marginal revenue was hundred thousand dollars per year