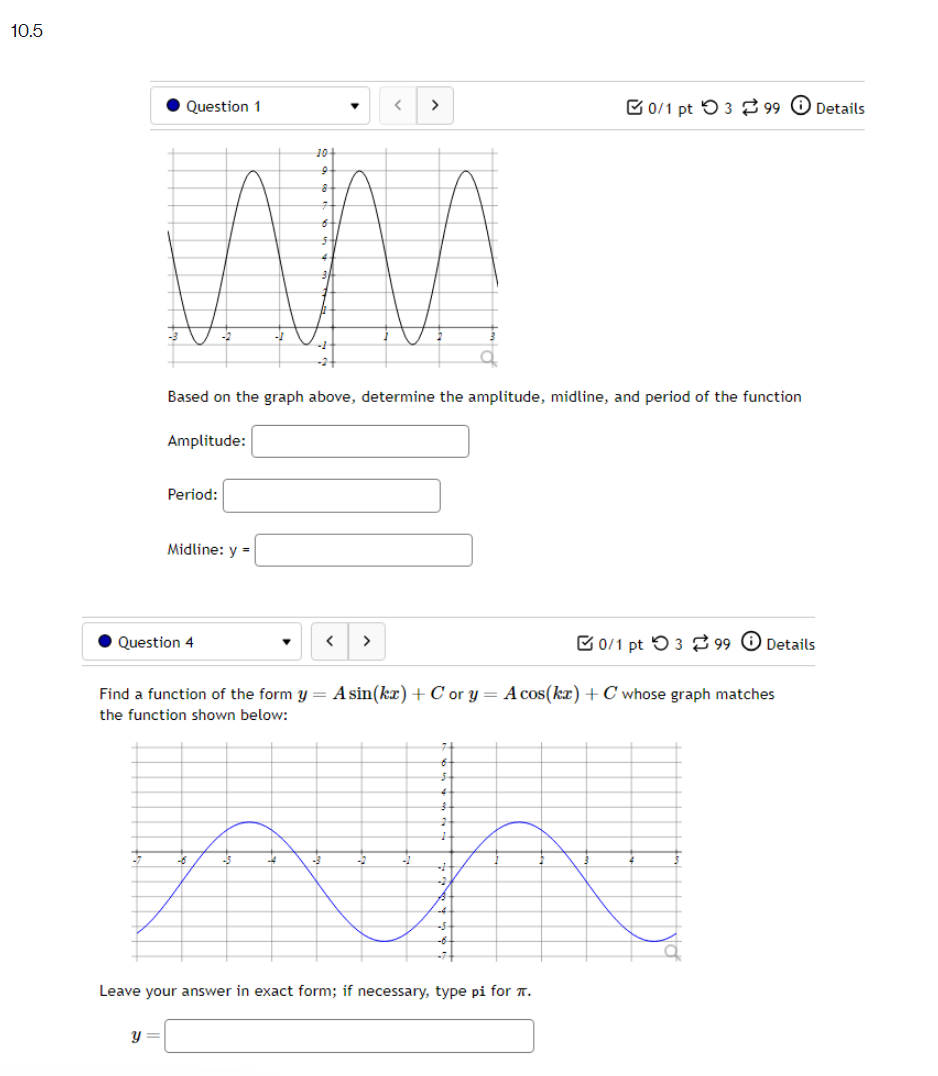
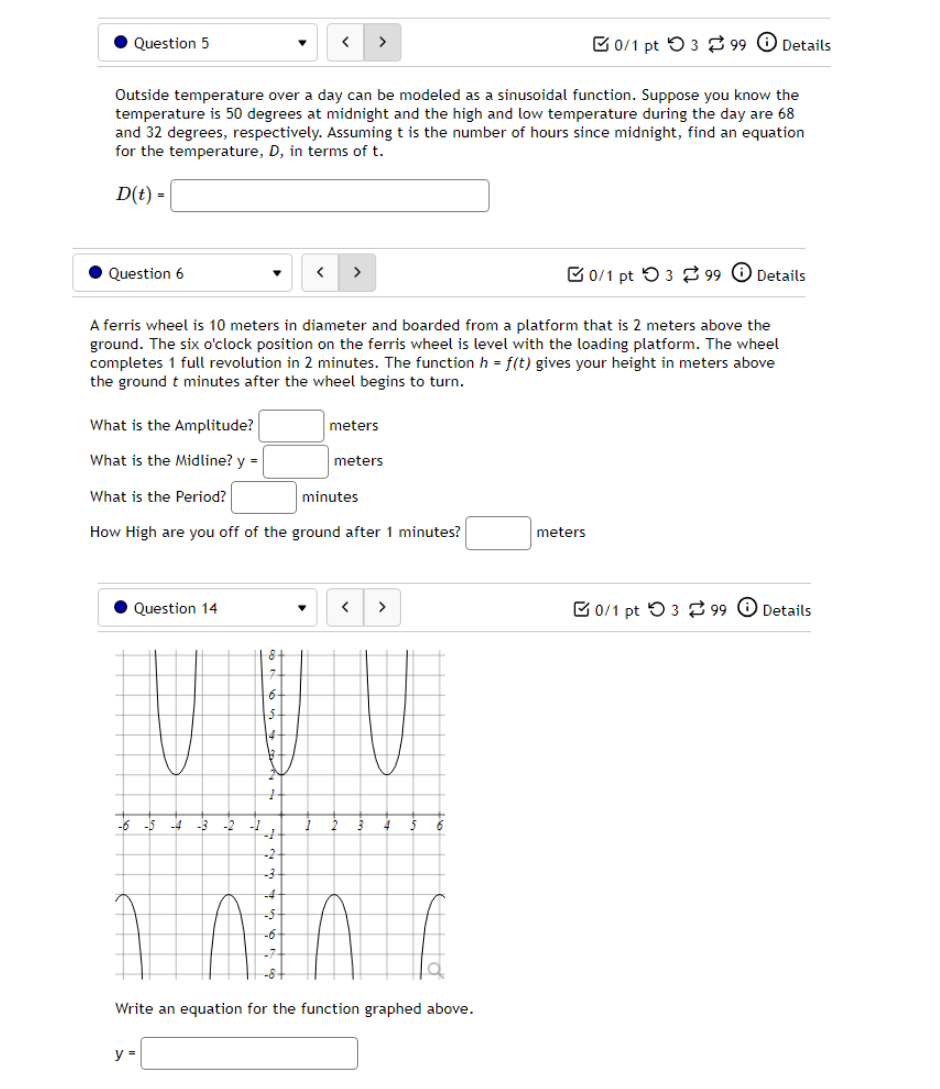
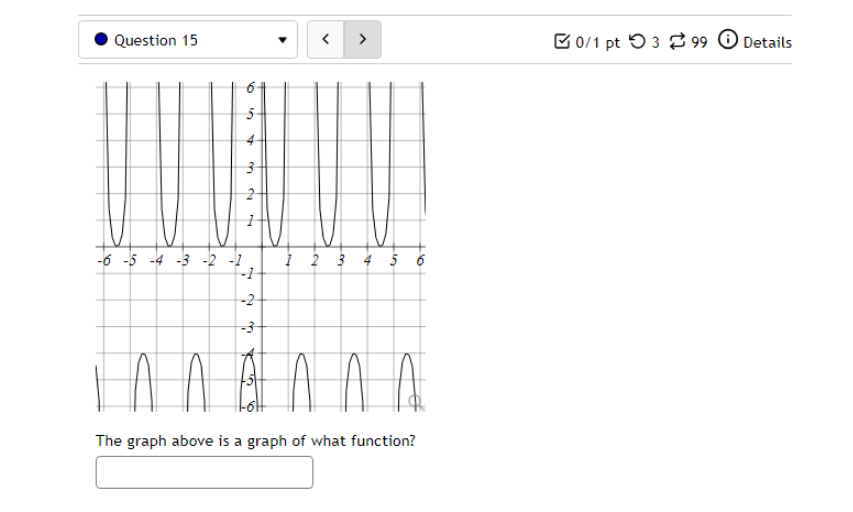
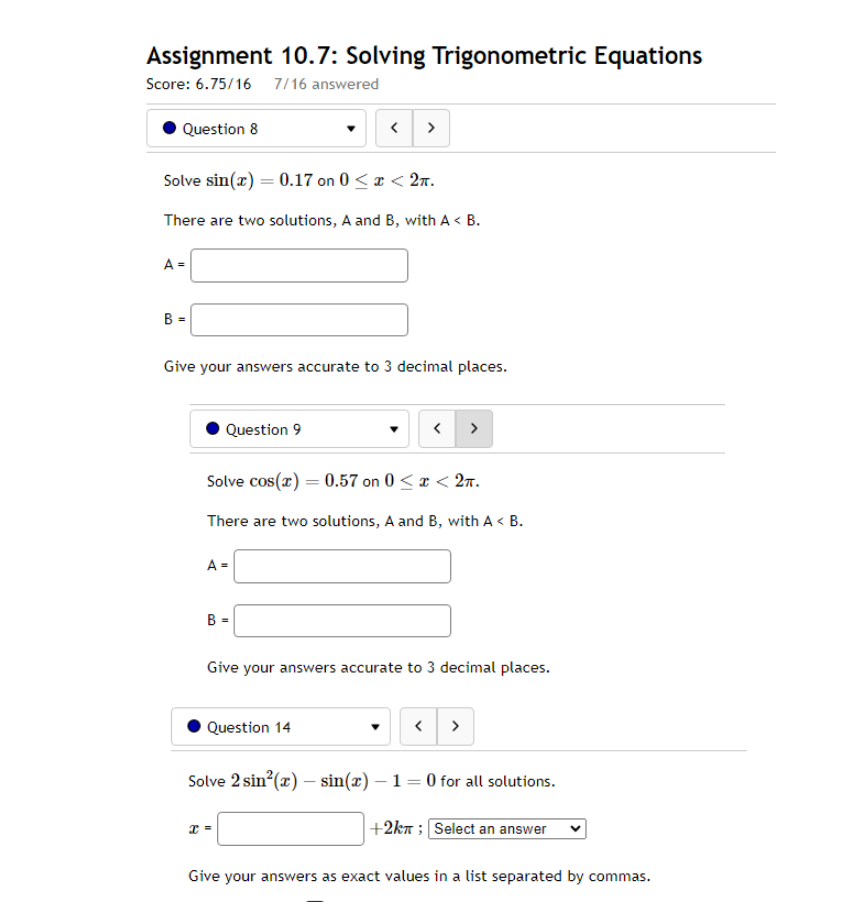
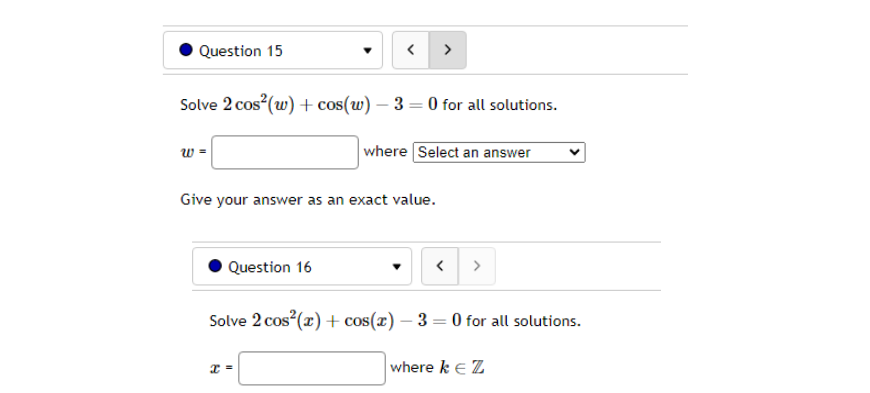
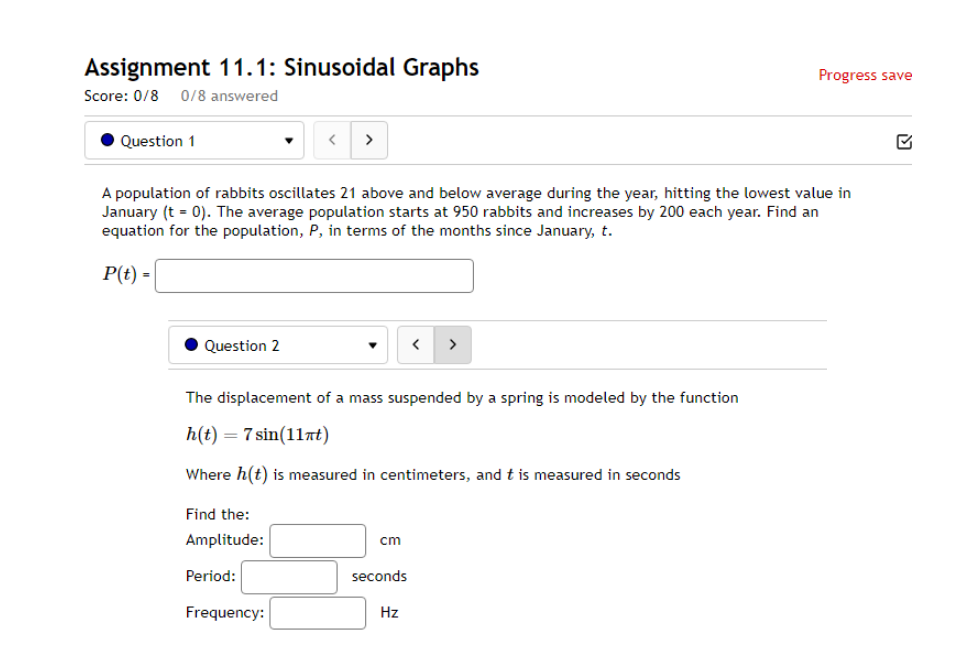
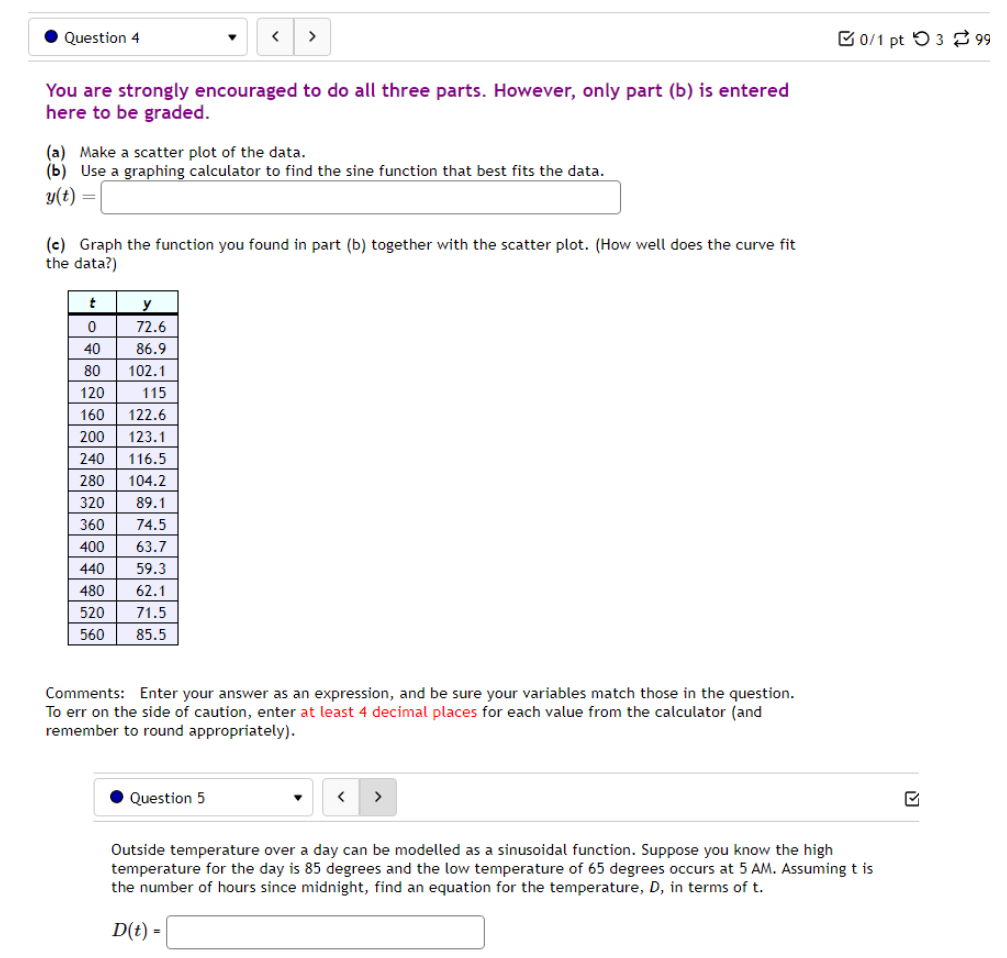
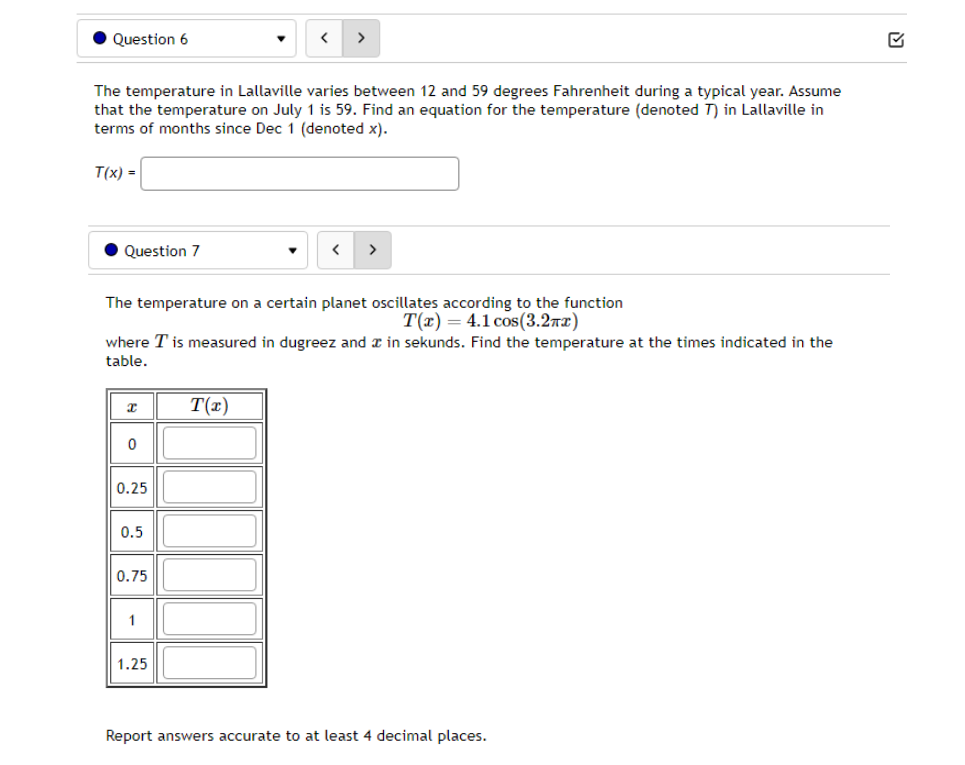
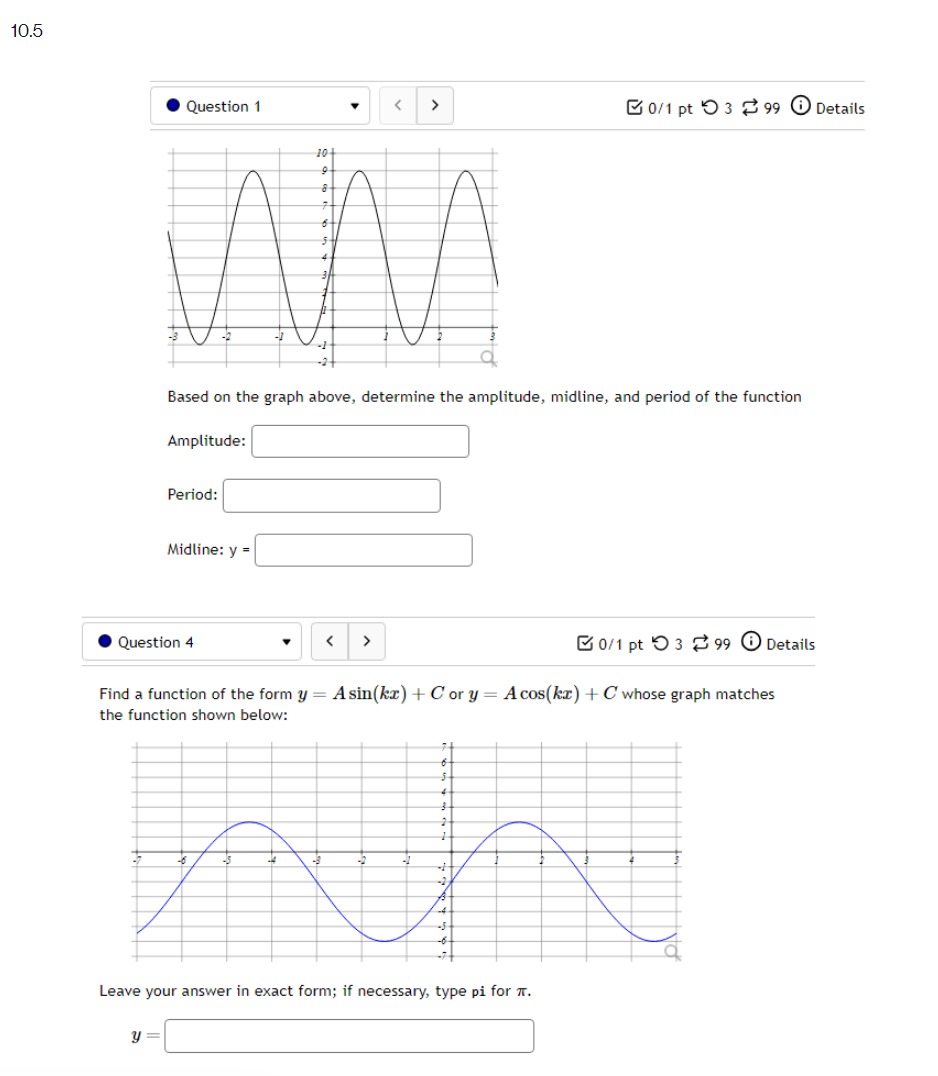
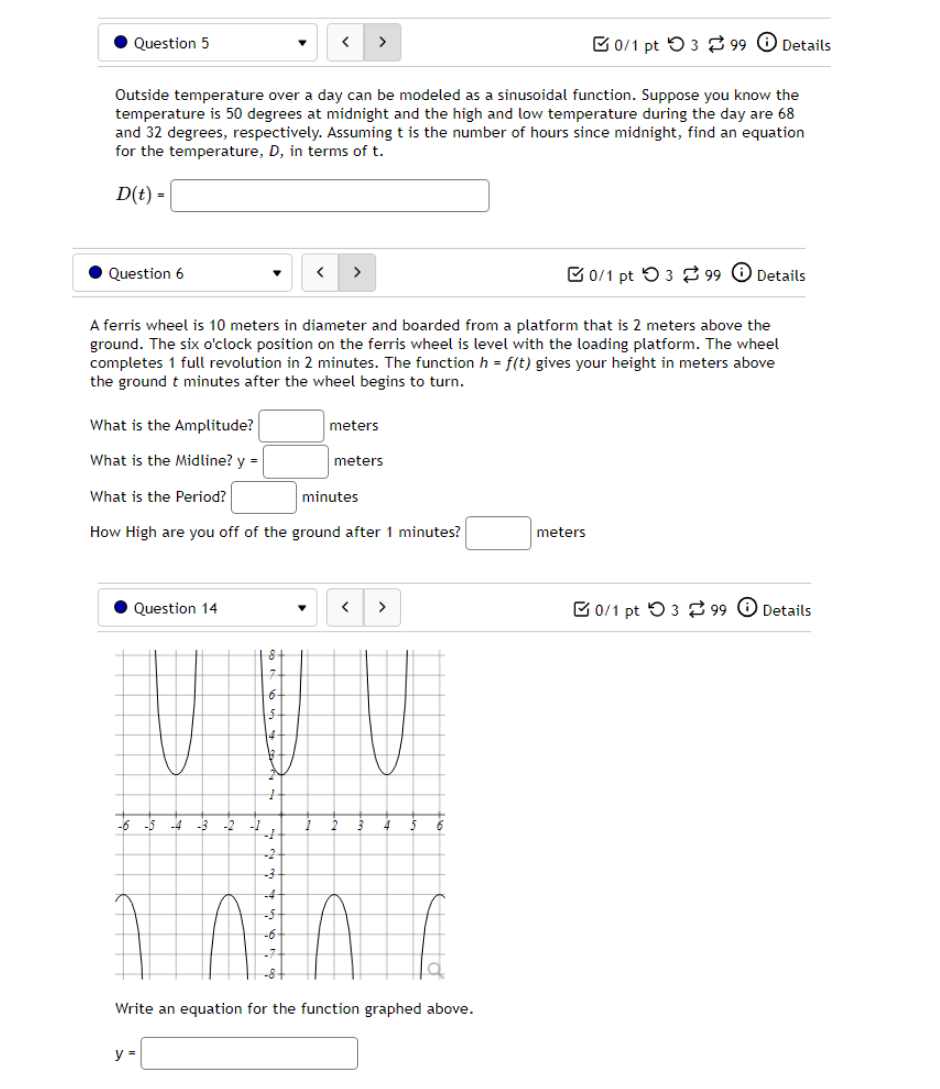
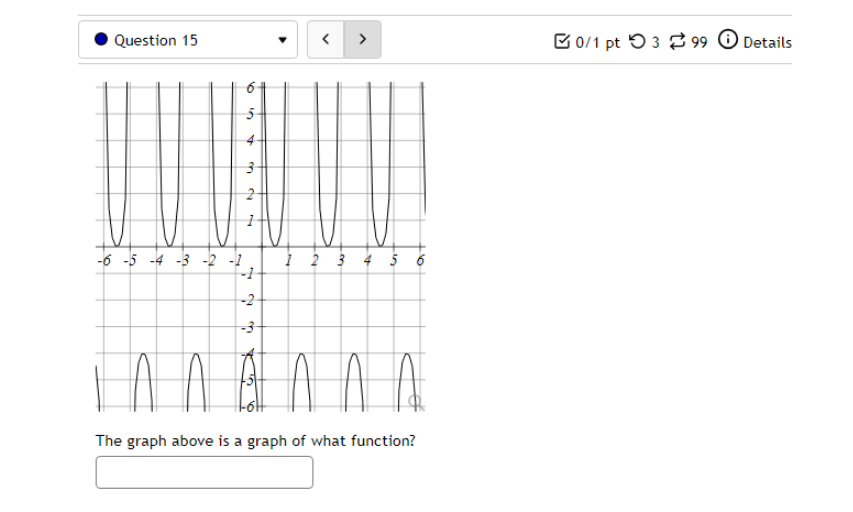
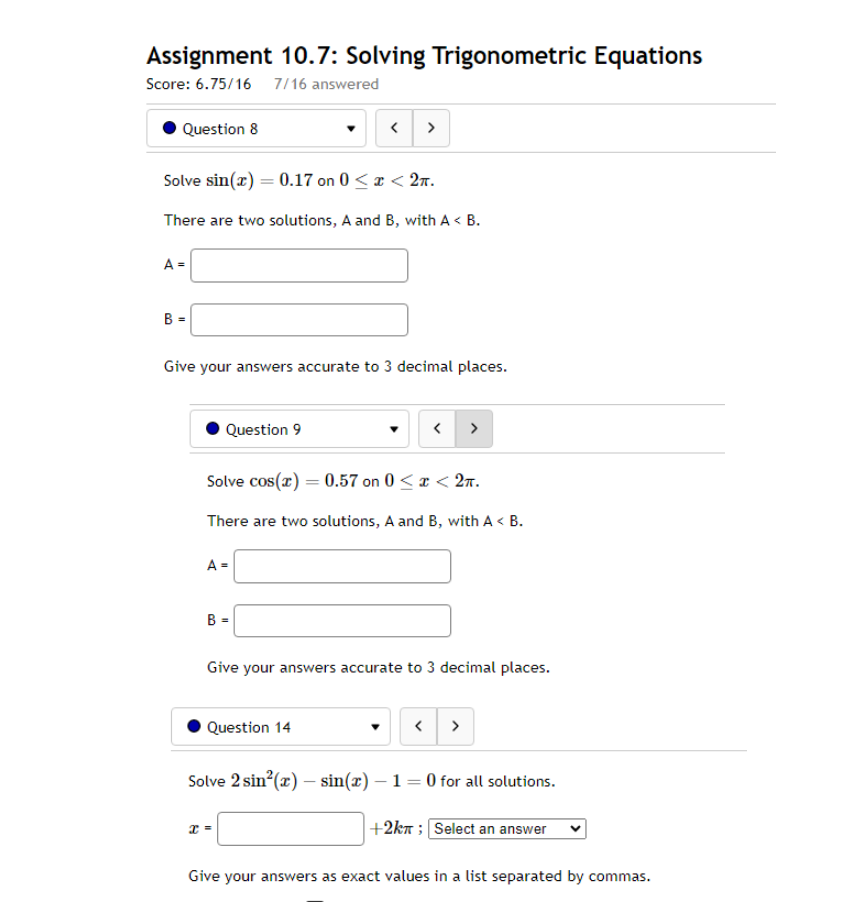
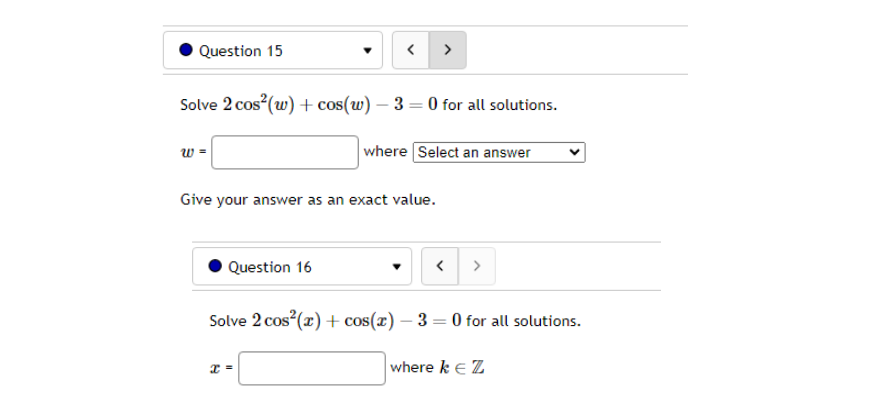
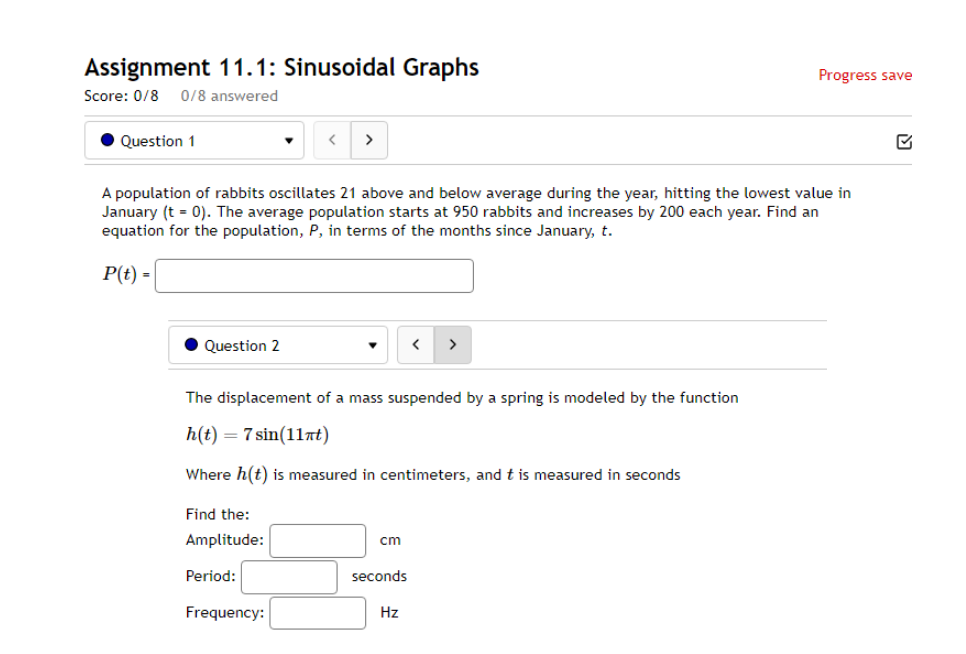
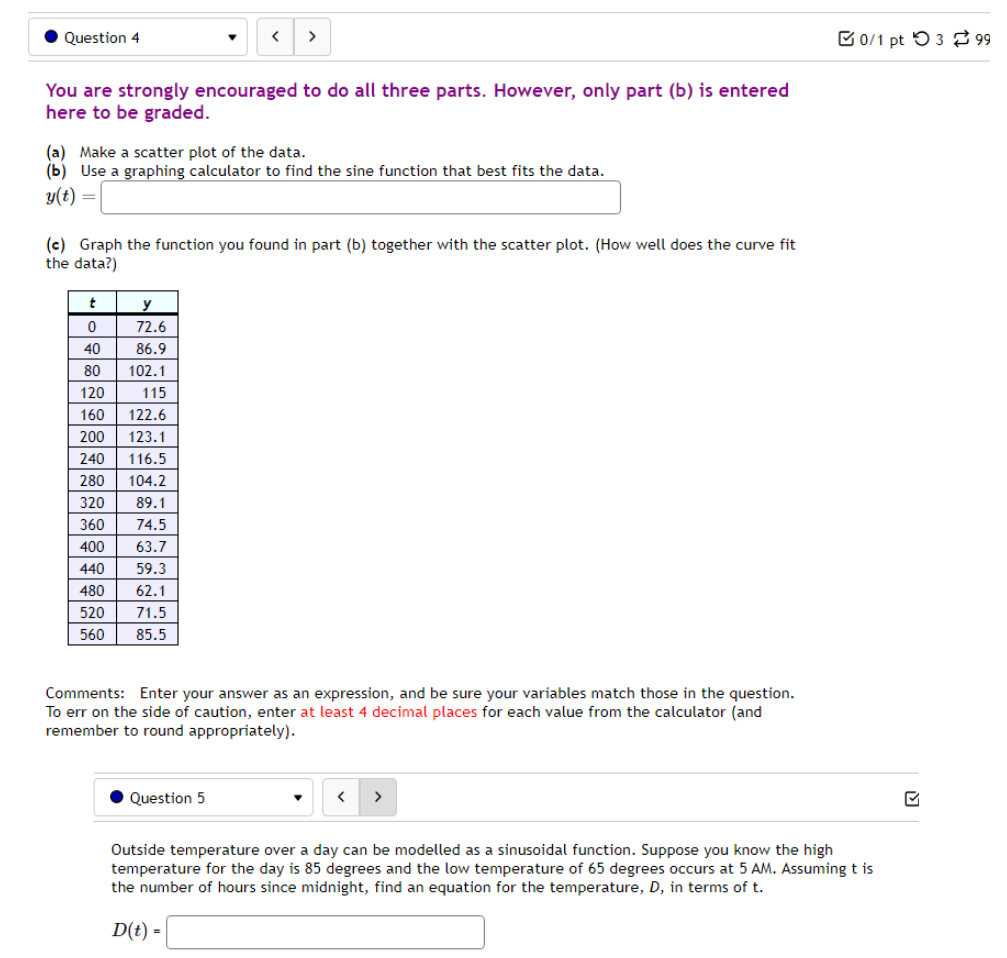
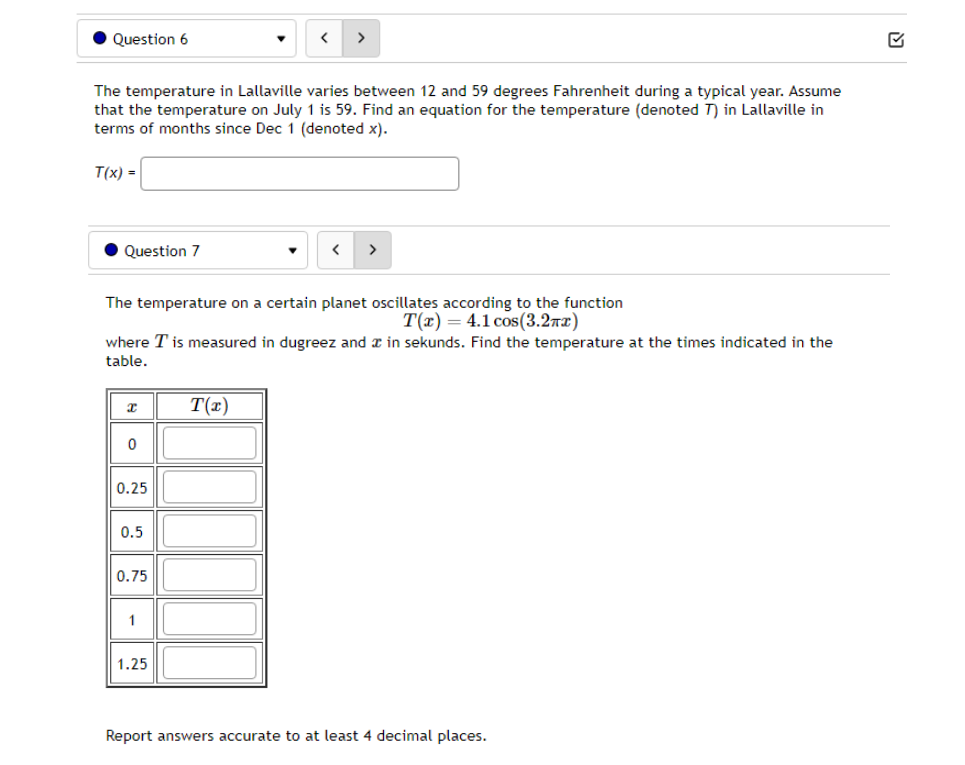
10.5 '. Question 1 ' B 011 pt '0 3 23' 99 (3 Details Find a function of the form y = Asin'tz) + Car y = Acos(k:l:) + those graph matches the function shown below: Leave your answer in exact form; if necessary, type pi for 7:. y: . Question 5 0/1 pt 9 3 99 0 Details Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the temperature is 50 degrees at midnight and the high and low temperature during the day are 68 and 32 degrees, respectively. Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t. D(t) = .Question 6 Go/1 pt 9 3 99 @ Details A ferris wheel is 10 meters in diameter and boarded from a platform that is 2 meters above the ground. The six o'clock position on the ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 2 minutes. The function h = f(t) gives your height in meters above the ground t minutes after the wheel begins to turn. What is the Amplitude? meters What is the Midline? y = meters What is the Period? minutes How High are you off of the ground after 1 minutes? meters . Question 14 > 0/1 pt 9 3 99 0 Details -6 -5 -4 -3 -2 -1 Write an equation for the function graphed above. y =. Question 15 1" 'i 3' 3 W1 pt '0 3 2-3 99 O Details 45-5-4.3-2-1 1.23456 n2 n: i; in in m The graph above is a graph of what function? [1 Assignment 10.7: Solving Trigonometric Equations Score: 6.75/16 7/16 answered . Question 8 Solve sin() = 0.17 on 0 Solve 2 cos (x) + cos(x) - 3 = 0 for all solutions. T = where k E ZAssignment 1 1.1 : Sinusoidal Graphs Score: DIS 0: 8 answered Progress save I Questionl v B A population of rabbits oscillates 21 above and below average during the year, hitting the lowest value in January [t - D]. The average population starts at 950 rabbits and increases by 200 each year. Find an equation for the population, P. in terms of the months since January. t. Pm =| . Question 2 v The displacement of a mass suspended by a spring is modeled by the function Mt} : 751n(11:rrt) Where Mt) is measured in centimeters, and t is measured in seconds Find the: _ Amplitude: I cm Period: I I seconds Frequency: I H: (a) Make a scatter plot of the data. (b) Use a graphing calculator to find the sine function that best fits the data. y(t) = (c) Graph the function you found in part (b) together with the scatter plot. (How well does the curve fit the data?) t y 0.15 9.39 0.3 15.58 0.45 21.3 0.6 24.45 0.75 23.89 0.9 19.81 1.05 13.71 1.2 7.83 1.35 4.32 1.5 4.46 1.65 8.21 1.8 14.19 1.95 20.21 2. 1 24.07 2.25 24.34 Comments: Enter your answer as an expression, and be sure your variables match those in the question. To err on the side of caution, enter at least 4 decimal places for each value from the calculator (and remember to round appropriately).I Question 4 - E on pt '0 3 B 99 You are strongly encouraged to do all three parts. However, only part (b) is entered here to be graded. (a) Make a scatter plot of the data. "3} Use a graphing calculator to find the sine function that best fits the data. Hit) = l ] {1:} Graph the function you found in part {b} together with the scatter plot. {How well does the curve fit the data?) - IE!!- IE]- I55]- Eil- Comments: Enter your answer as an expression, and be sure your variables match those in the question. To err on the side of caution, enter at least 4 decimal places for each value from the calculator {and remember to round appropriately]. . Question 5 v 3 Outside temperature over a dag.r can be modelled as a sinusoidal function. Suppose you know the high temperature for the day is 35 degrees and the low temperature of 65 degrees occurs at 5 AM. Assuming t is the number of hours since midnight, find an equation for the temperature. D, in terms of t. D(t) =| . Question 6 The temperature in Lallaville varies between 12 and 59 degrees Fahrenheit during a typical year. Assume that the temperature on July 1 is 59. Find an equation for the temperature (denoted 7) in Lallaville in terms of months since Dec 1 (denoted x). T(x) = . Question 7 The temperature on a certain planet oscillates according to the function T(x) = 4.1 cos(3.2TI) where T' is measured in dugreez and I in sekunds. Find the temperature at the times indicated in the table. I T(x) 0 0.25 0.5 0.75 1.25 Report answers accurate to at least 4 decimal places