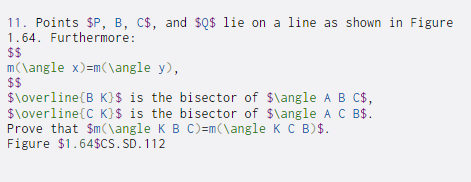
11. Points $P, B, C$, and $0$ lie on a line as shown in Figure 1.64. Furthermore: $$ m( angle x)=m(\angle y), $$ $\overline{B K}$ is the bisector of $\angle A B C$, $\overline{C K}$ is the bisector of $\angle A C B$. Prove that $m(\angle K B C)=n(\angle K C B) $. Figure $1.64$CS.SD. 112 11. Points $P, B, C$, and $0$ lie on a line as shown in Figure 1.64. Furthermore: $$ m( angle x)=m(\angle y), $$ $\overline{B K}$ is the bisector of $\angle A B C$, $\overline{C K}$ is the bisector of $\angle A C B$. Prove that $m(\angle K B C)=n(\angle K C B) $. Figure $1.64$CS.SD. 112