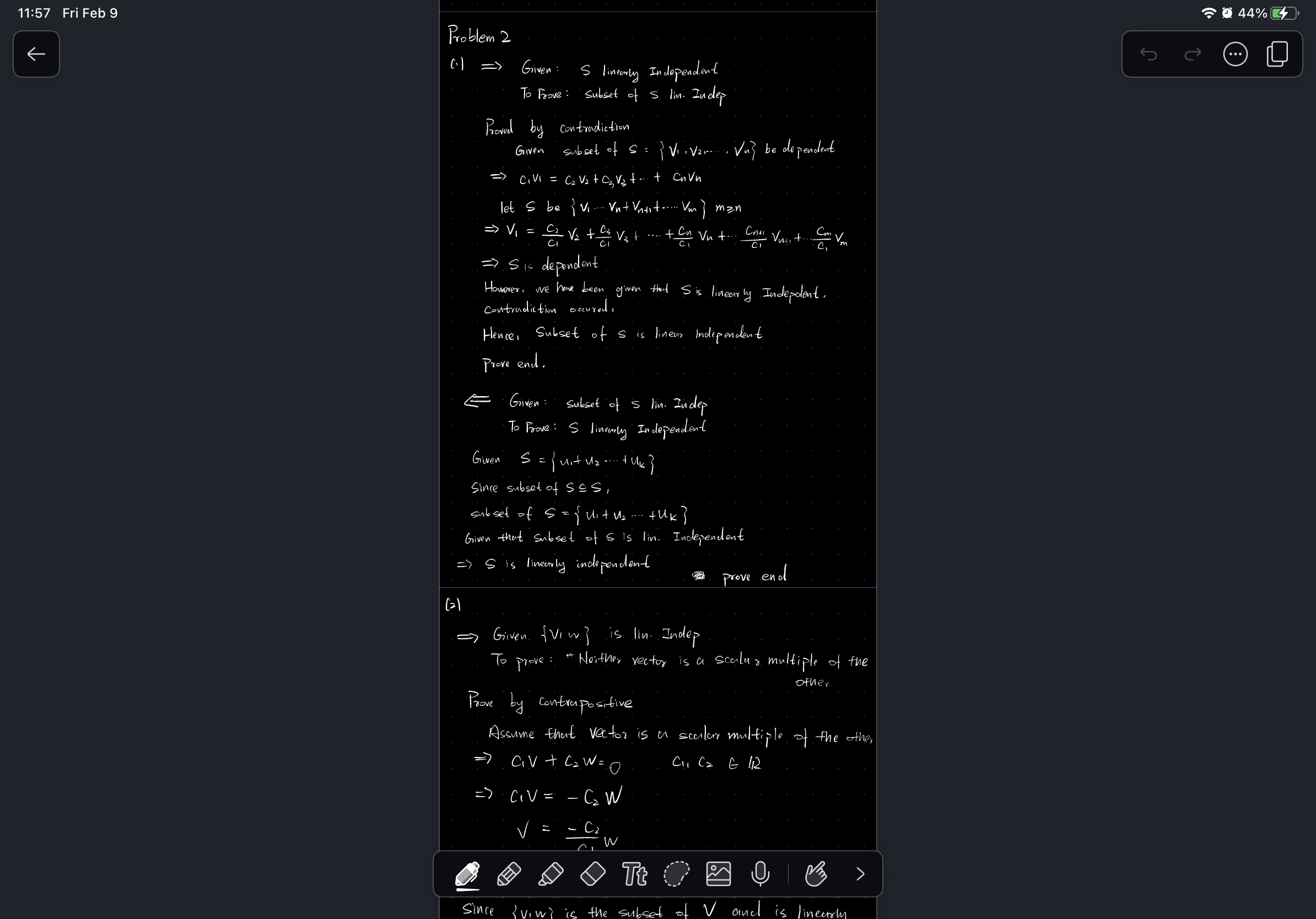
11:57 Fri Feb 9 2 44% Problem 2 Given : S linearly Independent To Frove : Subset of S Im. Indep Proved by contradiction Given subset of S : Viva ... Vng be dependent => CIVI = CV3+ Q,Vat ..+ Cnn let S be { Vi . Vn+ Visit ... Vm ) man S is dependent However , we have been given that S is linearly Indepdent . Contradiction occured , Hence, Subset of S is linear independent Prove end . Given : subset of S li. Indep To Frove : S linewily Independent Given S = ( Uit Uz ... + Uk ] Since subset of SCS , subset of S = { uit us .. + UK ] Given that Subset of S Is lin . Independent =) S is linearly independent prove end = Given {Viw] is lin. Indep To prove : " Neither vector is a sculas multiple of the ofher Prove by contrapositive Assume that vector is a secular multiple of the other - CV + CW = 0 CI Ca G 12 3 CIV = - CW V= - C2 w Tt > Since the V and is lineetsProblem 2. . (1) Show that a subset S of a vector space V is linearly independent if and only if every subset of S is linearly independent. (2) Suppose v, w are vectors in a vector space V. Show that {v,w} is linearly independent if and only if neither vector is a scalar multiple of the other