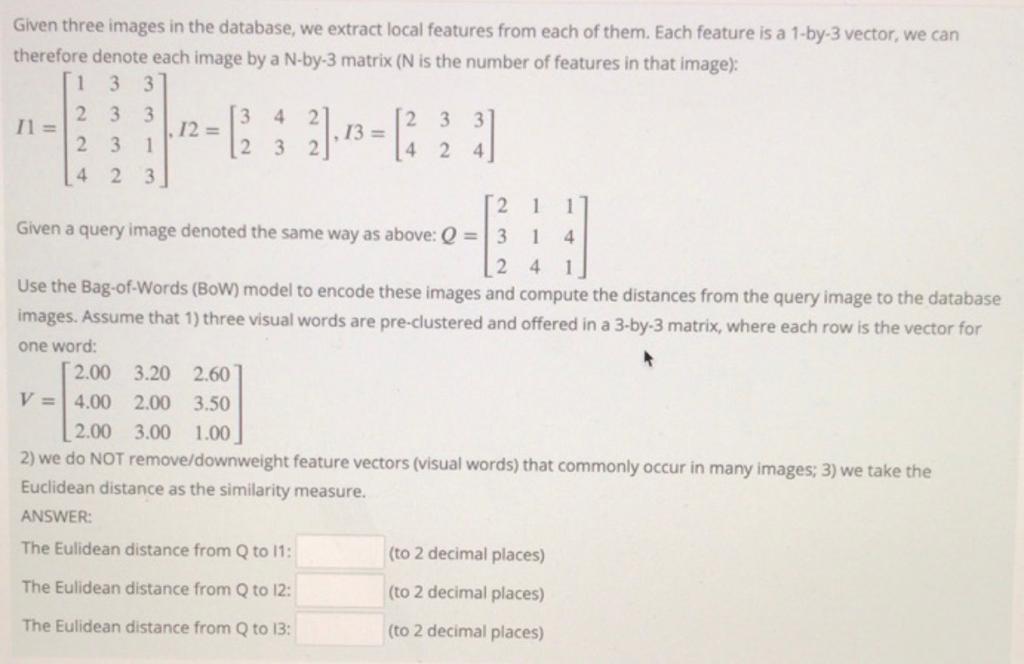
12 = Given three images in the database, we extract local features from each of them. Each feature is a 1-by-3 vector, we can therefore denote each image by a N-by-3 matrix (N is the number of features in that image): 1 3 3 2 3 3 3 4 2 12. 3 3 11 = 13 = 2 3 1 2 3 2 4 2 4 4 2 3 2 1 1 Given a query image denoted the same way as above: Q = 3 1 4 2 4 1 Use the Bag-of-Words (BOW) model to encode these images and compute the distances from the query image to the database images. Assume that 1) three visual words are pre-clustered and offered in a 3-by-3 matrix, where each row is the vector for one word: 2.00 3.20 2.60 V =4.00 2.00 3.50 2.00 3.00 1.00 2) we do NOT remove/downweight featu vectors (visual words) that commonly occur in many images; 3) we take the Euclidean distance as the similarity measure. ANSWER: The Eulidean distance from Q to 11: (to 2 decimal places) The Eulidean distance from Q to 12: (to 2 decimal places) The Eulidean distance from Q to 13: (to 2 decimal places)