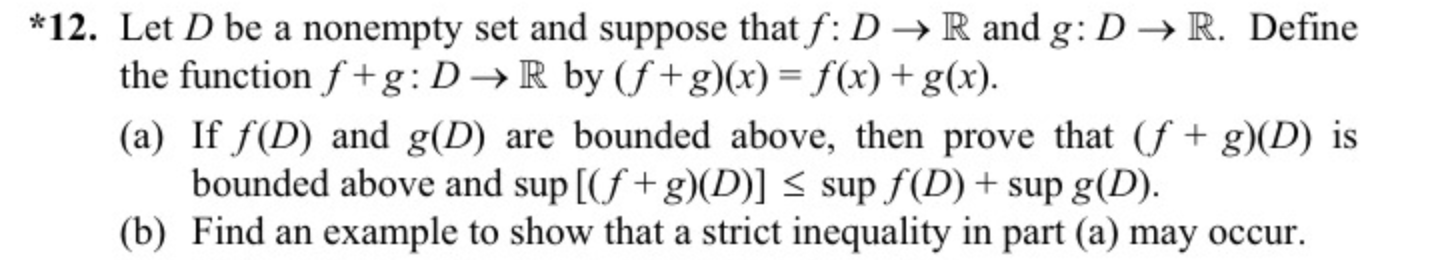
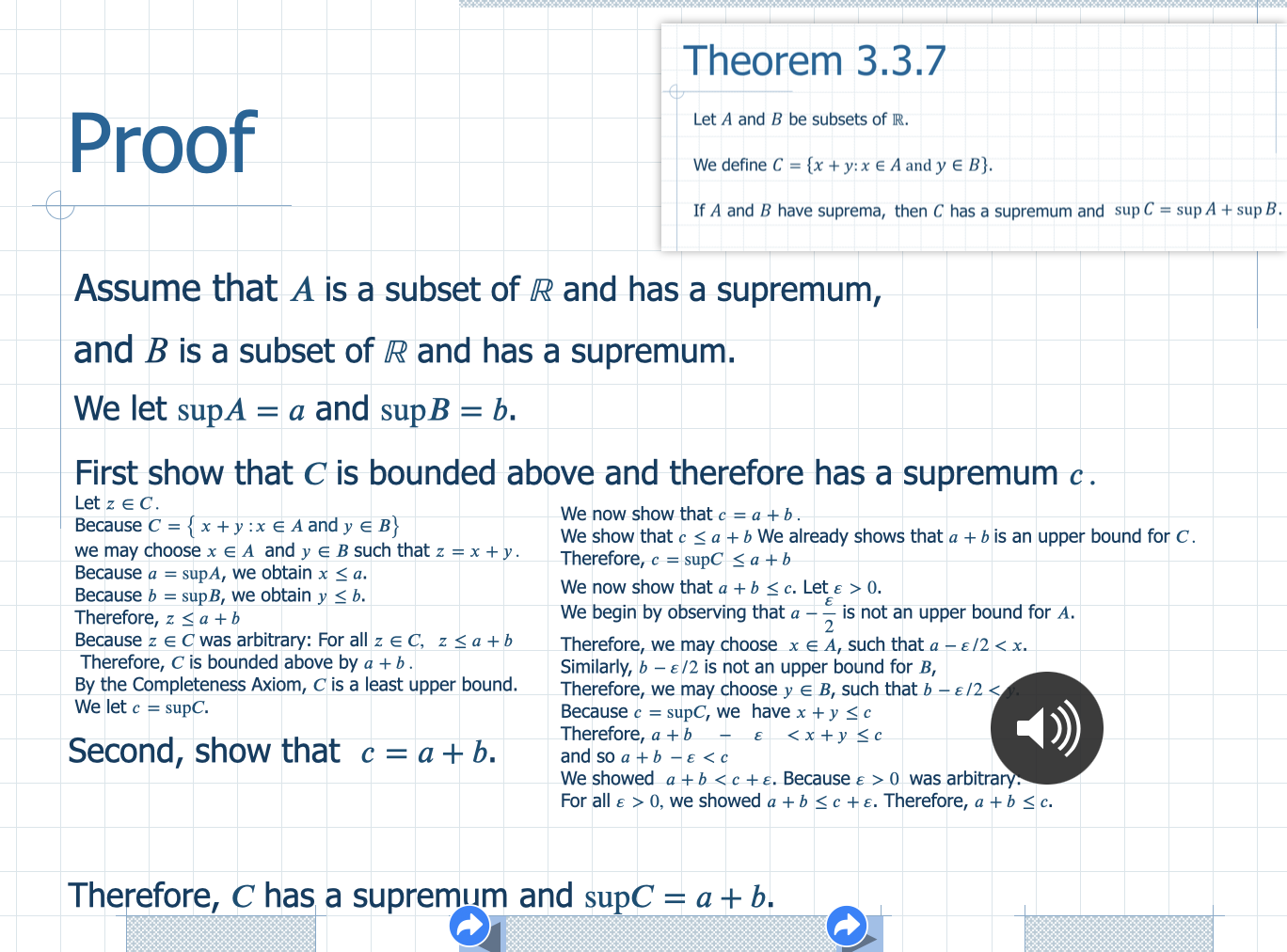
*12. Let D be a nonempty set and suppose that f/: D R and g: D R. Define the function f+g: D R by (f +2)(x) = f(x) + g(x). (a) If f(D) and g(D) are bounded above, then prove that (f + g)(D) is bounded above and sup [( f + g)(D)] 0. Therefore, z sa +b We begin by observing that a - - is not an upper bound for A. Because z E C was arbitrary: For all z E C, z S a + b Therefore, we may choose x E A, such that a - E/2 0 was arbitrary. For all & > 0, we showed a + b z. (b) For each x > 0 and each y R, there exists n A, such that nx > y. (c) For each x > 0, there exists n N, such that 0