Question: . (12 points) A vial in a biochemistry lab has a population of genetically engineered micro-organisms called the HAPPY-Q. A scientist wishes to keep track

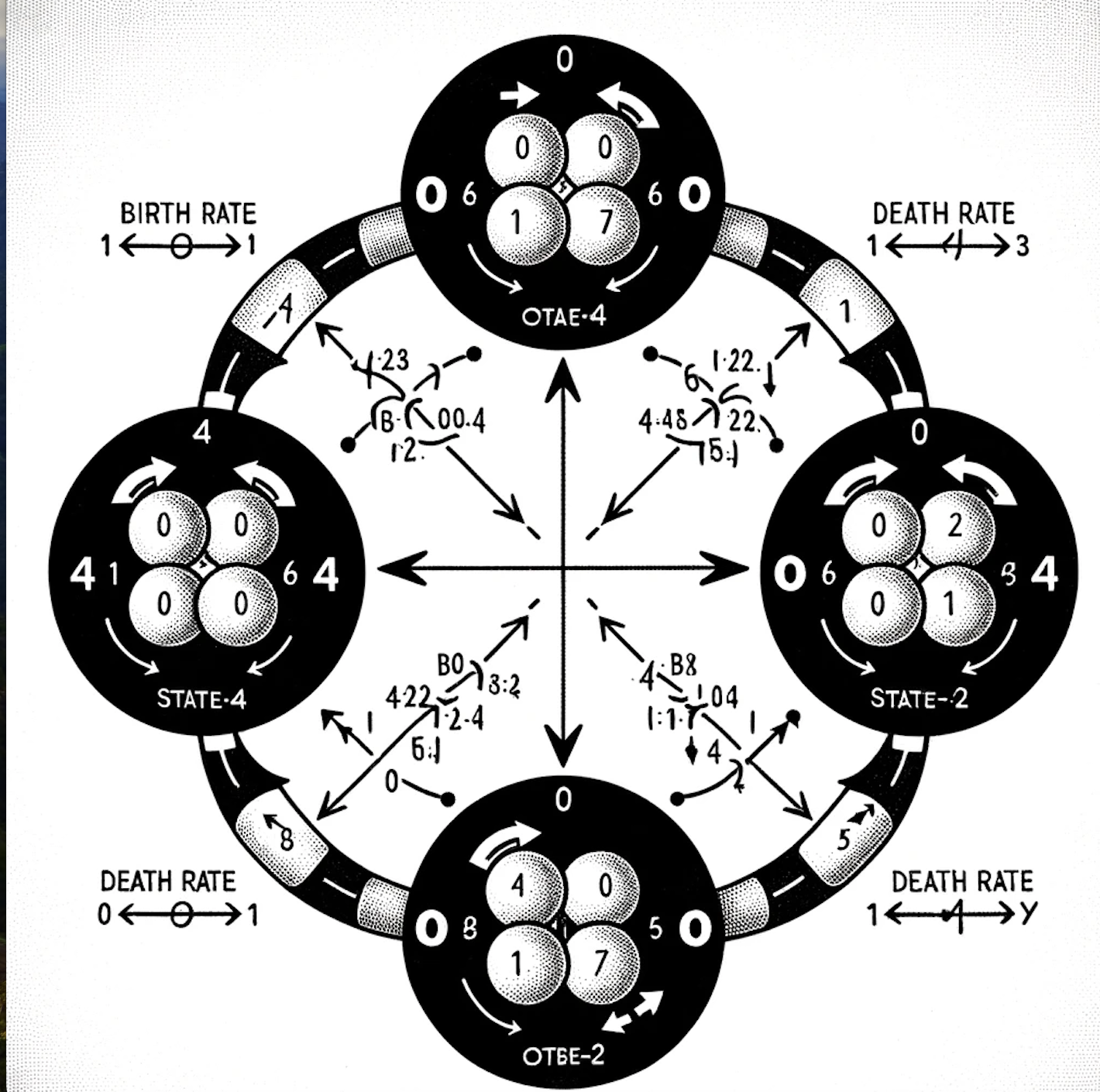
. (12 points) A vial in a biochemistry lab has a population of genetically engineered micro-organisms called the HAPPY-Q. A scientist wishes to keep track of the size of this population. A new HAPPY-Q individual can enter this population in three ways (i) each existing HAPPY-Q individual can split into two after an exponentially distributed amount of time with parameter A, (i1) the vial is connected by a tube to a population of HAPPY-X micro-organisms that can create one HAPPY-Q individual after an exponentially distributed amount of time with parameter A, and (ii1) the vial is also connected by a tube to a population of HAPPY-Y micro-organisms that can create one HAPPY-Q individual after an exponentially distributed amount of time with parameter 2. Each HAPPY-Q individual lives an exponentially distributed amount of time with parameter p. The scientist has added a population control chemical which does not allow the HAPPY-Q population to grow beyond four (i.e. the maximum population 1s four). a. (5 points) Model the number of HAPPY-Q in the vial as a birth-death process by drawing its rate diagram. Then suppose A=1, p=1. \f

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The Global Tea and Organic Juice companies have merged. The following information has been collected for the Consolidation Project. 1. Compute the expected time for each activity. 2. Compute the...

(12 points) A vial in a biochemistry lab has a population of genetically engineered micro-organisms called the HAPPY-Q. A scientist wishes to keep track of the size of this population. A new HAPPY-Q...

37.2021 X C 1) Describe The Vertical Chain Fo x Study.com - Search for courses, I x +...

Nucleon 1) Describe the vertical chain for biotechnology productions. What "make" decisions has Nucleon already made? What "buy" decisions has it already made? Evaluate these decisions. 2) Draw a...

chegg.com/homework-help/questions-and-answers/1-describe-vertical-chain-biotechnology-productions-make The CRP-1 Project: Current Applications Since Nucleon's founding, its main development project...

WA-3- Valuation; Part 1 - Fundamental Method. Use ONLY Excd for this WA, and make sure I can trace ALL your calculations. I can only do this if you did NOT plug in the end answers. If done via Word...

1. Making an Unpaid Intern Sort Things (12 points) An unpaid intern named Carl is tasked with placing a number of Important Chemicals in their appropriate containers. The Chemicals are as follows,...

someone please help, i will rate you! i forgot to weigh my sample of toluene after a distillation process. i started with 30 mL of the solution and was able to determine the volume of ethyl acetate....

Name ______________________ Mathematical Modeling in Life Sciences Spring 2017 ANSC 448 / IB 487 / STAT 458 Exam 1 (100 points) "Without passion, all the skill in the world won't lift you above...

5. Your patient is actively seizing. Your benzodiazepine of choice is midazolam, which comes in a multidose vial of 20 mL. The concentration of the vial is 5 mg/ml. The first dose of midazolam is...

Question 12 points) The medical starron shudder Island was an averare of B7 vials of Thorarin every we weekly demand is normally distributed with a standard deviation of 12 was the ordering costs...

Using EES (or other) software, investigate the effect of extraction pressure on the performance of an ideal regenerative Rankine cycle with one open feedwater heater. Steam enters the turbine at 15...

Using the following information, calculate cost of goods sold for the year ended December 31, 2014. Merchandise inventory (January 1, 2014)..............................................................

When a taxpayer disagrees with CRA's interpretation of the Income Tax Act, what options does the taxpayer have? Option A Escalate the issue to the Minister of Finance Option B File a court case to...

please answer only if you know programming language is c++ For this lab, your objective is to define the functions below. Define the void function SwapNodes () that takes three generic type Node...