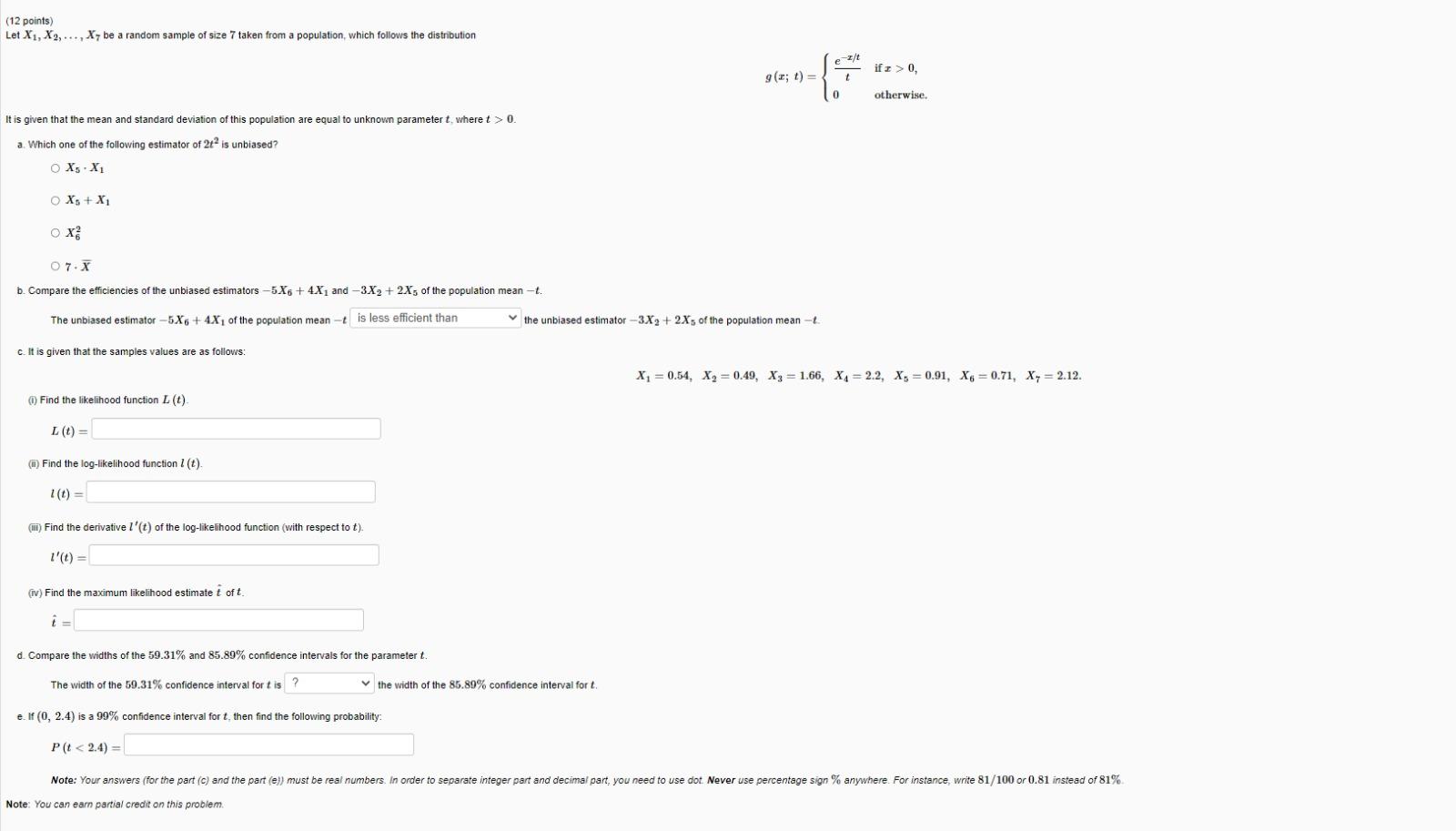
(12 points) Let X1, X2, ..., X7 be a random sample of size 7 taken from a population, which follows the distribution 9 (2; 1) = if x > 0, otherwise. It is given that the mean and standard deviation of this population are equal to unknown parameter t, where t > 0. a. Which one of the following estimator of 2t is unbiased? O X5 . X1 O Xs + X1 OX 0 7 . X b. Compare the efficiencies of the unbiased estimators -5X6 + 4X, and -3X2 + 2Xs of the population mean -t. The unbiased estimator -5X6 + 4.X, of the population mean - |is less efficient than the unbiased estimator -3X2 + 2X's of the population mean - c. It is given that the samples values are as follows: X1 = 0.54, X2 = 0.49, X3 = 1.66, X4 = 2.2, Xs = 0.91, X6 = 0.71, X7 = 2.12. () Find the likelihood function L (t) L(t) = () Find the log-likelihood function 1 (t). 1 (t) = (mi) Find the derivative I'(t) of the log-likelihood function (with respect to t). I'(t) = (iv) Find the maximum likelihood estimate t of t. 1 = d. Compare the widths of the 59.31% and 85.89% confidence intervals for the parameter t. The width of the 59.31% confidence interval for t is ? the width of the 85.89% confidence interval for t. e. If (0, 2.4) is a 99% confidence interval for t, then find the following probability: P (t