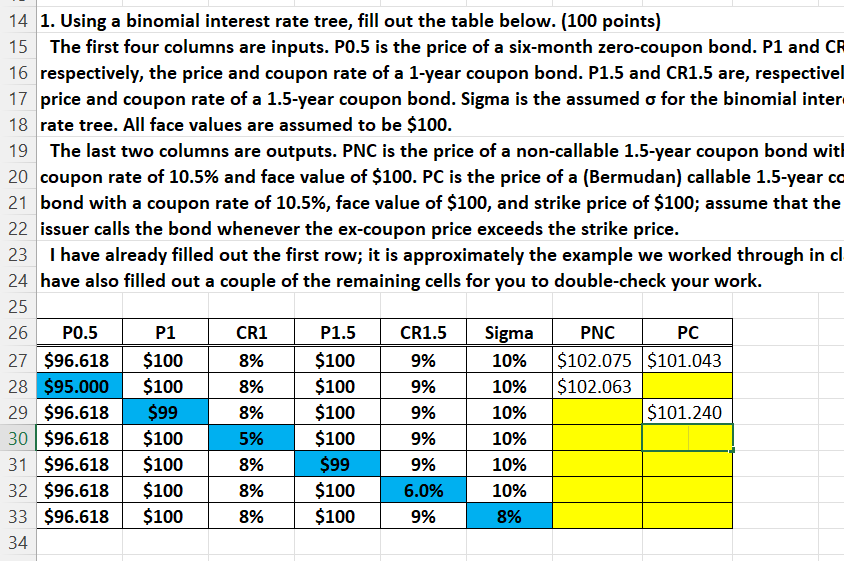
14 1. Using a binomial interest rate tree, fill out the table below. (100 points) 15 The first four columns are inputs. P0.5 is the price of a six-month zero-coupon bond. P1 and CR 16 respectively, the price and coupon rate of a 1-year coupon bond. P1.5 and CR1.5 are, respectivel 17 price and coupon rate of a 1.5-year coupon bond. Sigma is the assumed o for the binomial inter 18 rate tree. All face values are assumed to be $100. 19 The last two columns are outputs. PNC is the price of a non-callable 1.5-year coupon bond with 20 coupon rate of 10.5% and face value of $100. PC is the price of a (Bermudan) callable 1.5-year co 21 bond with a coupon rate of 10.5%, face value of $100, and strike price of $100; assume that the 22 issuer calls the bond whenever the ex-coupon price exceeds the strike price. I have already filled out the first row; it is approximately the example we worked through in cl 24 have also filled out a couple of the remaining cells for you to double-check your work. 25 26 P0.5 P1 27 $96.618 $100 28 $95.000 $100 29 $96.618 $99 30 $96.618 $100 31 $96.618 $100 32 $96.618 $100 33 $96.618 $100 34 CR1 P1.5 8% $100 8% $100 8% 5% 8% 8% 8% $100 $100 $99 $100 $100 CR1.5 Sigma 9% 9% 9% 9% 9% 6.0% 9% PNC PC 10% $102.075 $101.043 10% $102.063 10% 10% 10% 10% 8% $101.240