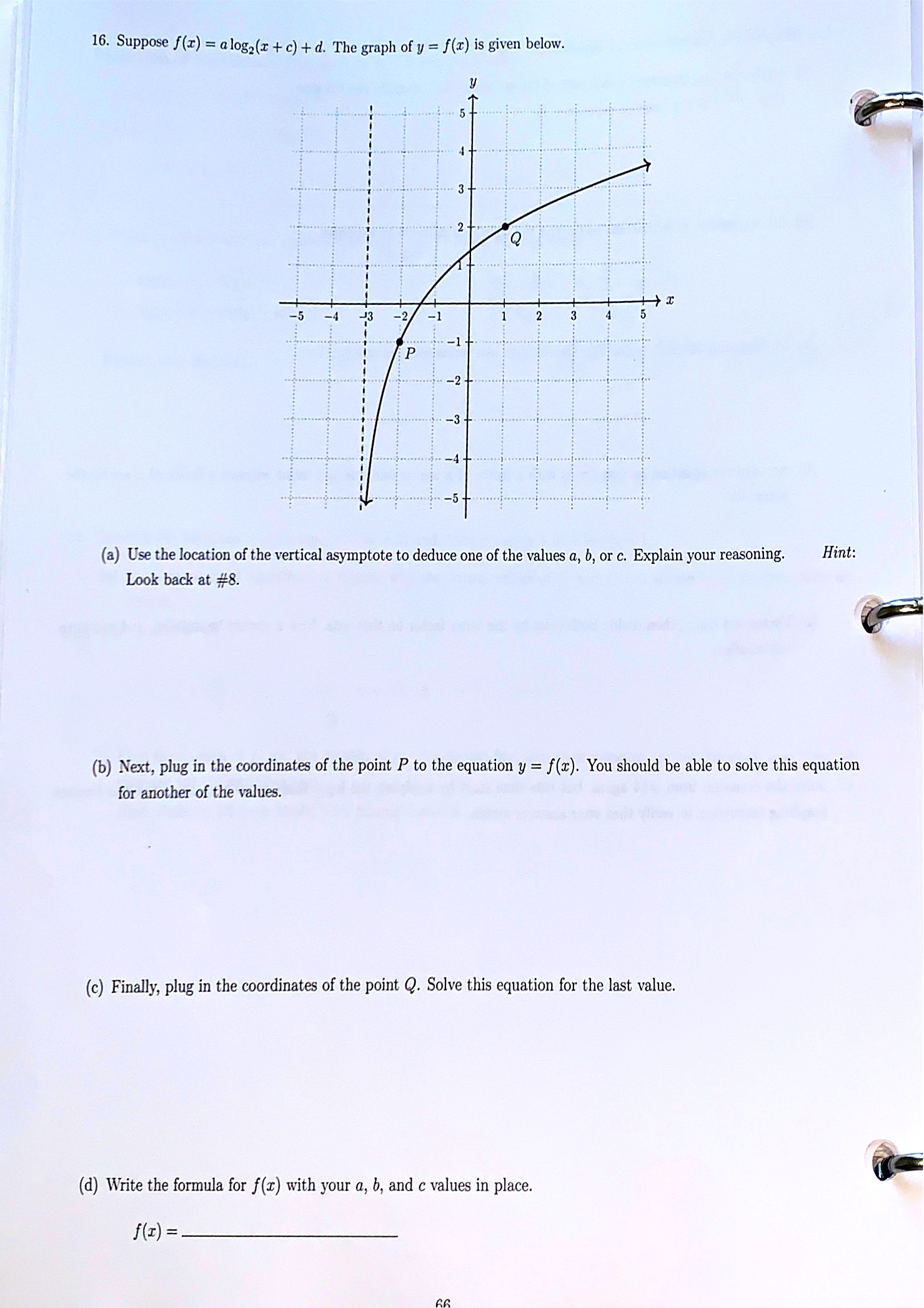
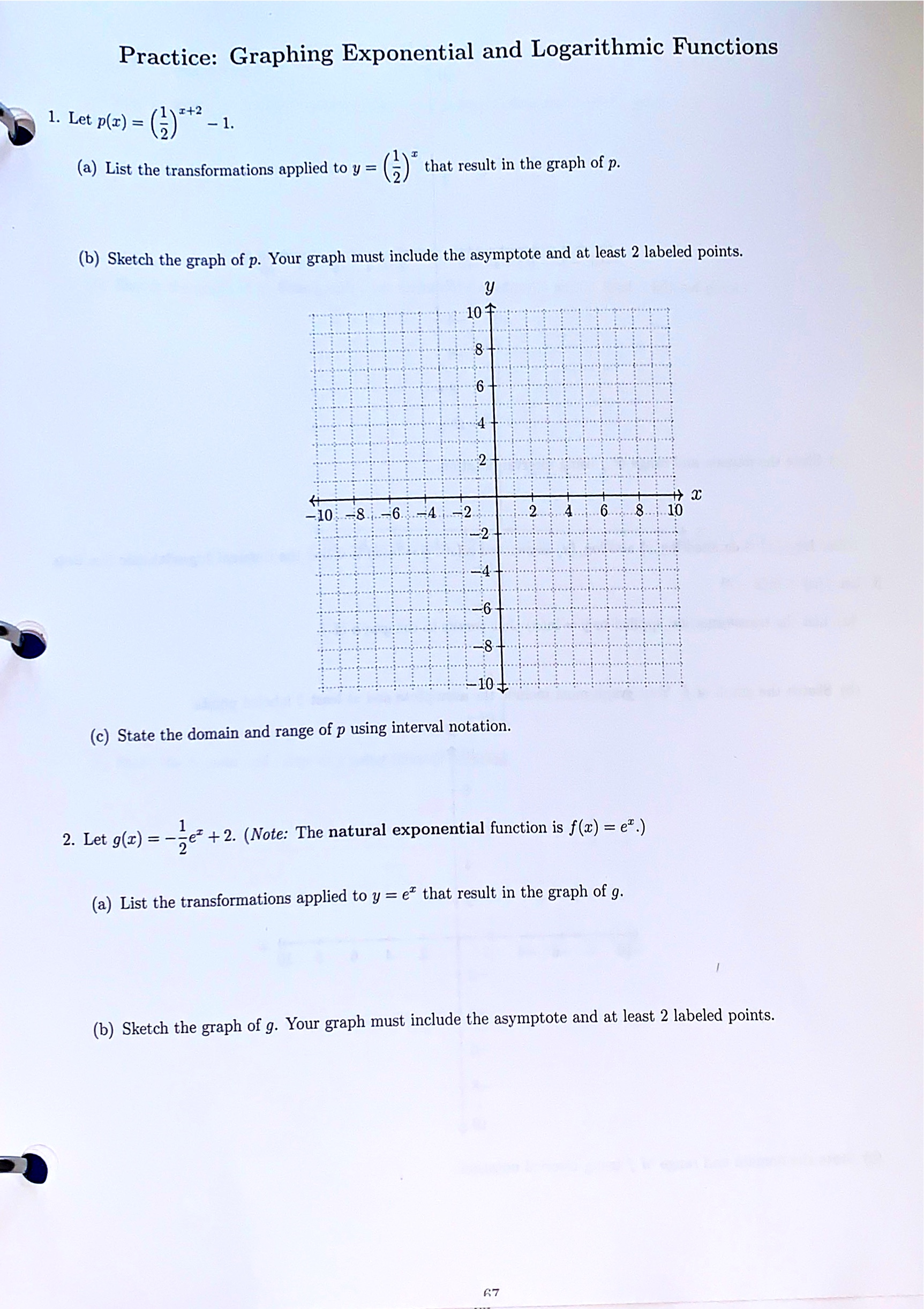
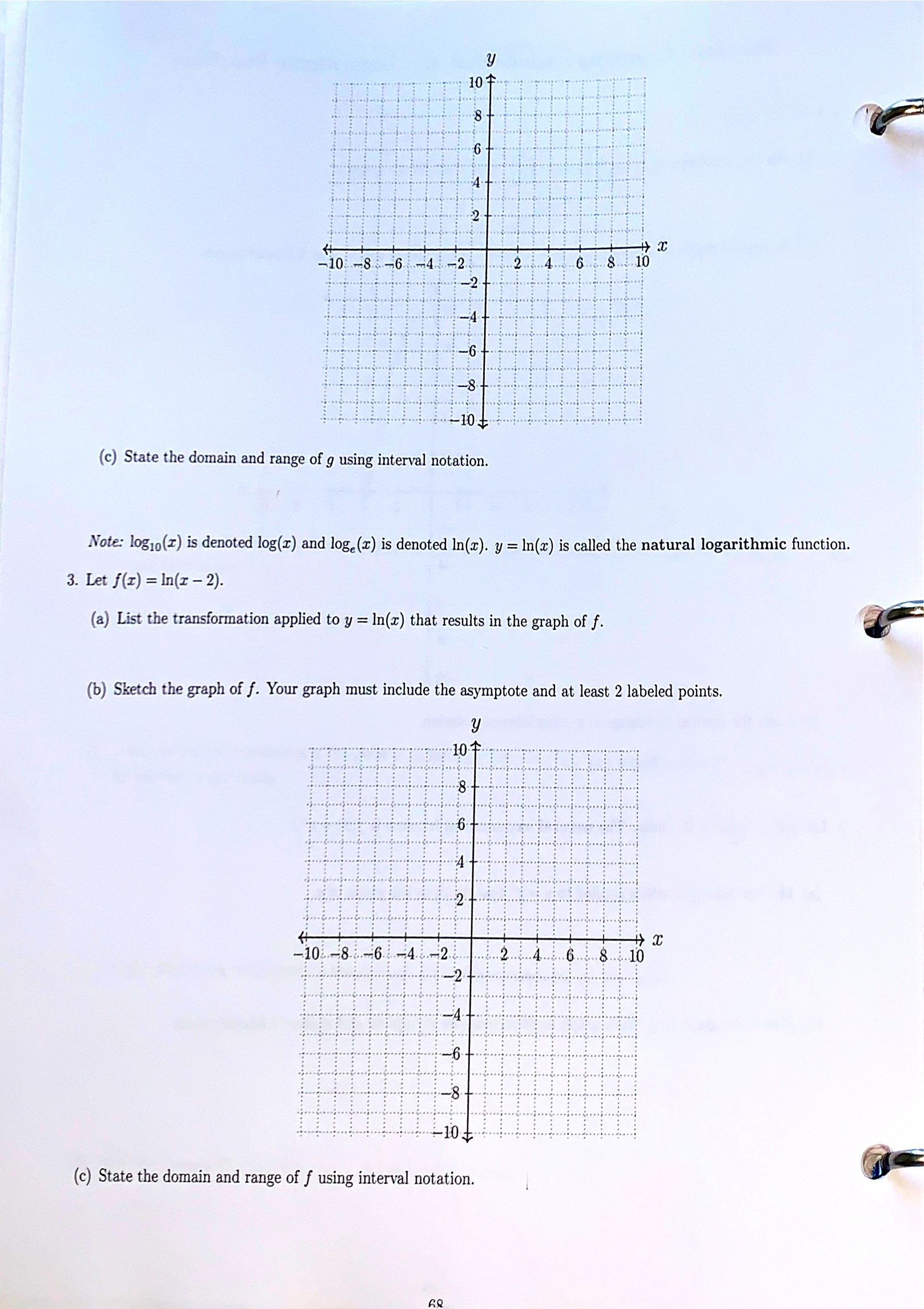
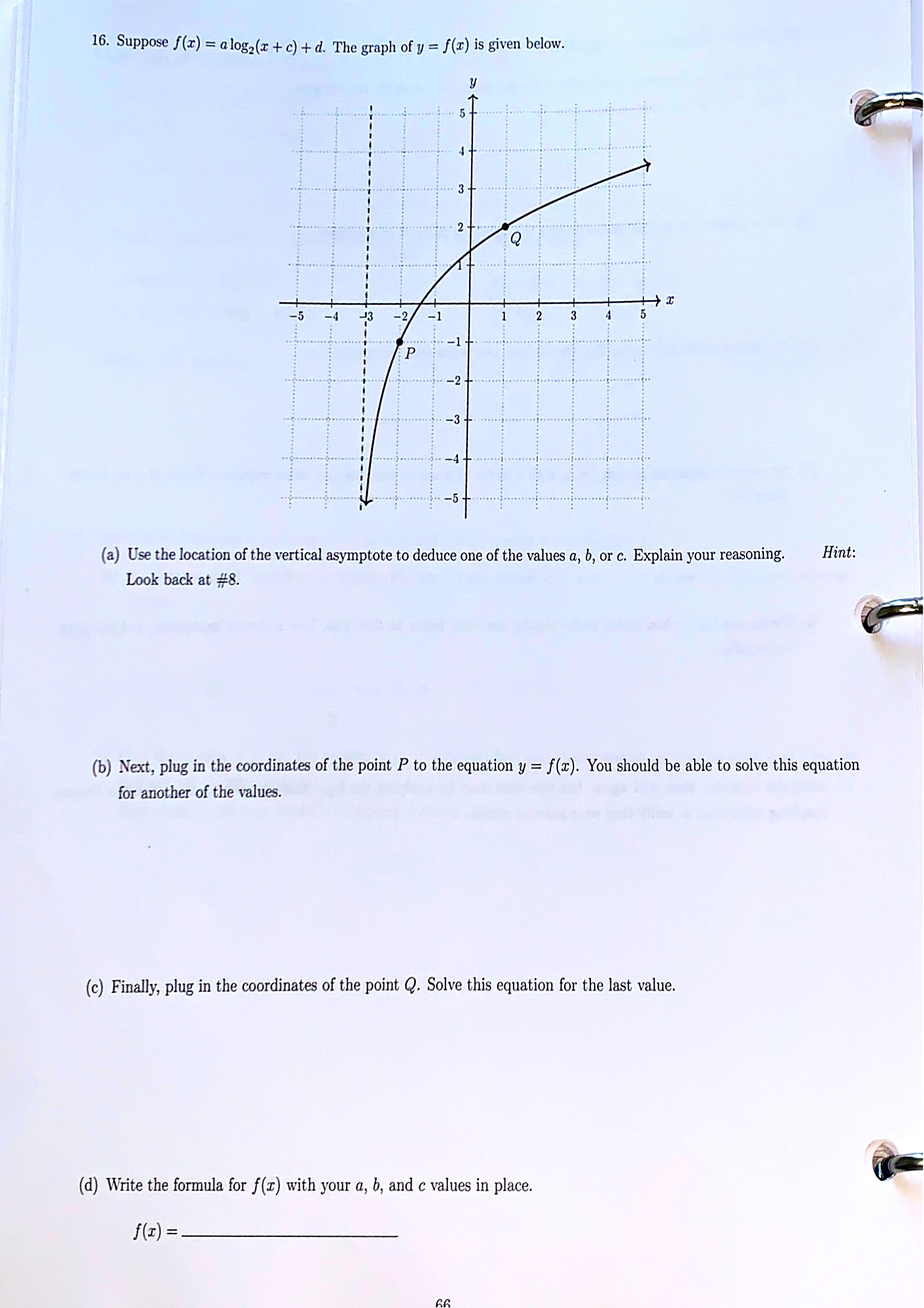
14. In this problem you will solve the equation 23+1 = 114-1. (a) Apply the log2 function to each side of the equation, then simplify the left side. Hint: 231+1 is the same as exp2 (3 + 1). (b) Use a property of logarithms to rewrite the right side without an exponent. (c) Multiply out the right side. You should have two terms containing log2(11). (d) Arrange the equation so that terms with a factor of x are on one side and terms without a factor of x are on the other side. (e) Factor out the z, then divide both sides by the other factor on that side. Now a should be isolated, and you have the solution. 15. Solve the equation from #14 again, but this time start by applying the log1 function to each side. Use the Desmos graphing calculator to verify that your answers match. 6516. Suppose f(x) = a log2(x + c) + d. The graph of y = f(x) is given below. 3 - 2 - -5 -4 - 2/ -1- ...... -2- -3- -4- . .... ..... ..... (a) Use the location of the vertical asymptote to deduce one of the values a, b, or c. Explain your reasoning. Hint: Look back at #8. (b) Next, plug in the coordinates of the point P to the equation y = f(x). You should be able to solve this equation for another of the values. (c) Finally, plug in the coordinates of the point Q. Solve this equation for the last value. (d) Write the formula for f(r) with your a, b, and c values in place. f ( I) =_Practice: Graphing Exponential and Logarithmic Functions h 1. Let 19(1) = G)\" _1_ (a) List the transformations applied to y = (g): that result in the graph of p. ('0) Sketch the graph of p. Your graph must include the asymptote and at least 2 labeled points. (c) State the domain and range of p using interval notation. 2. Let 9(3) = ;1)-e' + 2. (Note: The natural exponential function is f(2:) = em.) (a) List the transformations applied to y = e\"c that result in the graph of g. (b) Sketch the graph of g. Your graph must include the asymptote and at least 2 labeled points. (:7 10 + -2............... 0 -8 -6 -4 -2 ..10. (c) State the domain and range of g using interval notation. Note: log10(x) is denoted log(r) and log.(r) is denoted In(x). y = In(x) is called the natural logarithmic function. 3. Let f(x) = In(x - 2). (a) List the transformation applied to y = In(x) that results in the graph of f. (b) Sketch the graph of f. Your graph must include the asymptote and at least 2 labeled points. y ..... ... ..... ...j... ..... -10 -8-6-4-2. 1 6 8 10 3... .................... ... (c) State the domain and range of f using interval notation.Practice: Finding the Domain of a Logarithmic Function 5. Find the domain of each log function, expressed using interval notation. Your work for these problems must include an inequality and number line reasoning. (a) f(z) = 1082(x + 8) (b) h(x) = In(2x2 + x - 6) (c) g(z) = log v5x - 2 70perties properties of logarithms to expand each expression. Each logarithm should involve only one variable and should not have any radicals or exponents. You may assume that all variables are positive. (a) log(uzz?) (b) In(- (c) logs (2(2 + 7)5 2. Write the expression as a single logarithm. (a) 510g3(2 - 5) -310g3(2 + 2) (b ) 4in ( 7w + 1 ) + = In( w +5 ) -81n(w) (c) 7(10gc(w) - 310gc(x)) + 210gc(z) 71