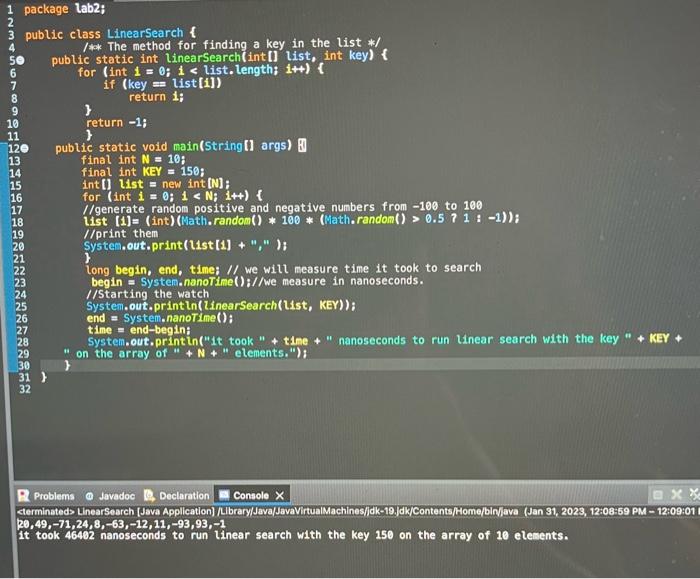
1.4. Proving with practice: best case We will add a small trick to get the best case: as the Key is known in advance, we will assign the first element to it. Technically we do not need to populate our array, just creating it (and population with zeros) is enough Modify the code as stated above. Keep running your simulations in analogous manner as in 1.3. for best case. Take a screenshot of your code and single output and insert your results in the same table. 1.5. Proving with practice: Average case It should be fine to generate the value of KEY randomly. You can choose its range yourself. Modify the code as stated above. Keep running your simulations in analogous manner as in 1.3. for the Average case. Take a screenshot of your code and single output and insert your results in the same table. public class LinearSearch 1 /** The method for finding a key in the list *J public static int linearsearch(int [] list, int key) f for (int 1=0;i0.571:1) ); //print them system.out,print(list [1] + ","); \} long begin, end, time; // we will measure time it took to search begin = system, nanotime(): ///we measure in nanoseconds. //starting the watch System,out.print ln(linearSearch(List, KEY)); end = System.nanoTime(); tine = end-begini System,out.printin("1t took " + tine + " nanoseconds to run linear search with the key " + KEY +