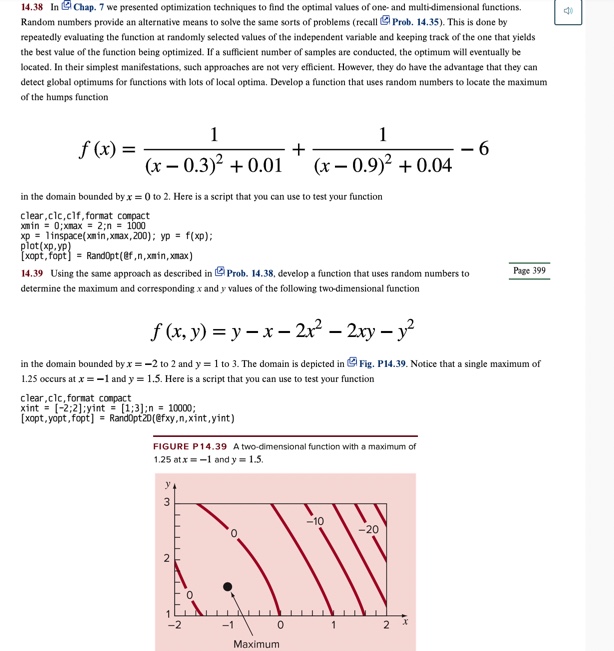
14.38 In ' Chap. 7 we presented optimization techniques to find the optimal values of one- and multi-dimensional functions. Random numbers provide an alternative means to solve the same sorts of problems (recall ( Prob. 14.35). This is done by repeatedly evaluating the function at randomly selected values of the independent variable and keeping track of the one that yields the best value of the function being optimized. If a sufficient number of samples are conducted, the optimum will eventually be located. In their simplest manifestations, such approaches are not very efficient. However, they do have the advantage that they can detect global optimums for functions with lots of local optima. Develop a function that uses random numbers to locate the maximum of the humps function f (x) = + - 6 (x - 0.3)2 + 0.01 (x - 0.9)2 + 0.04 in the domain bounded by x = 0 to 2. Here is a script that you can use to test your function clear, clc, clf, format compact xmin = 0;xmax = 2;n = 1000 xp = 1 inspace(xmin, xmax, 200]; yp = f(xp); plot (xp, yp] [ xopt, fopt] = RandOpt(@f , n, xmin, xmax) 14.39 Using the same approach as described in LO Prob. 14.38, develop a function that uses random numbers to Page 399 determine the maximum and corresponding x and y values of the following two-dimensional function f (x, y) =y-x- 2x2 - 2xy - 32 in the domain bounded by x = -2 to 2 and y = 1 to 3. The domain is depicted in ( Fig. P14.39. Notice that a single maximum of 1.25 occurs at x = -1 and y = 1.5. Here is a script that you can use to test your function clear , clc, format compact xint = [-2;2];yint = [1;3]:n = 10000; [xopt, yopt, fopt] = RandOpt20(@fxy, n, xint, yint) FIGURE P14.39 A two-dimensional function with a maximum of 1.25 atx = -1 and y = 1.5. -10 -20 0 -2 2 Maximum