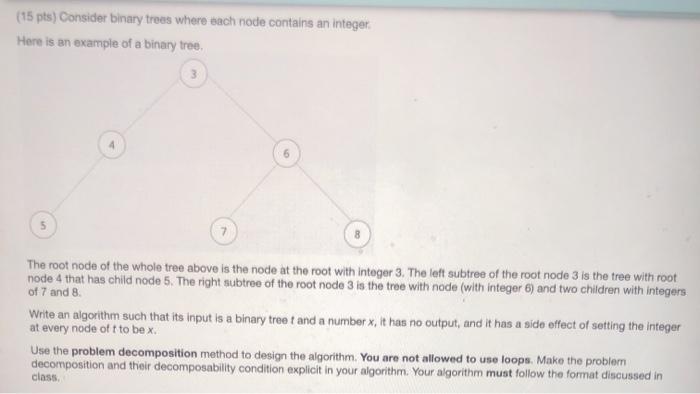
(15 pts) Consider binary trees where sach node contains an integer Here is an example of a binary tree, 3 5 7 The root node of the whole tree above is the node at the root with integer 3. The left subtree of the root node 3 is the tree with root node 4 that has child node 5. The right subtree of the root node 3 is the tree with node (with integer 6) and two children with integers of 7 and 8 Write an algorithm such that its input is a binary troet and a number x, it has no output, and it has a side effect of setting the integer at every node oft to be x. Use the problem decomposition method to design the algorithm. You are not allowed to use loops. Make the problem decomposition and their decomposability condition explicit in your algorithm. Your algorithm must follow the format discussed in class In your algorithm, no other functions are allowed except the following: function Ichild: its input is any treet and output is the left subtree of the root of t; function child: its input is any treet and output is the right subtree of the root of ti function empty; its input is any treet and output is true if treet is empty (.e., there are no nodes) and false otherwise; function set its inpqt is a treet and a number x, it has no output, and its side effect is to set the integer at the root node of 1 to be x. Hint: a tree can usually be decomposed as three parts: its root, its left tree and its right tree