Question: 16 Area and Sums: Problem 1 (10 points) The five rectangles in the graph below illustrate a ??7? + (select a description) Riemann sum for
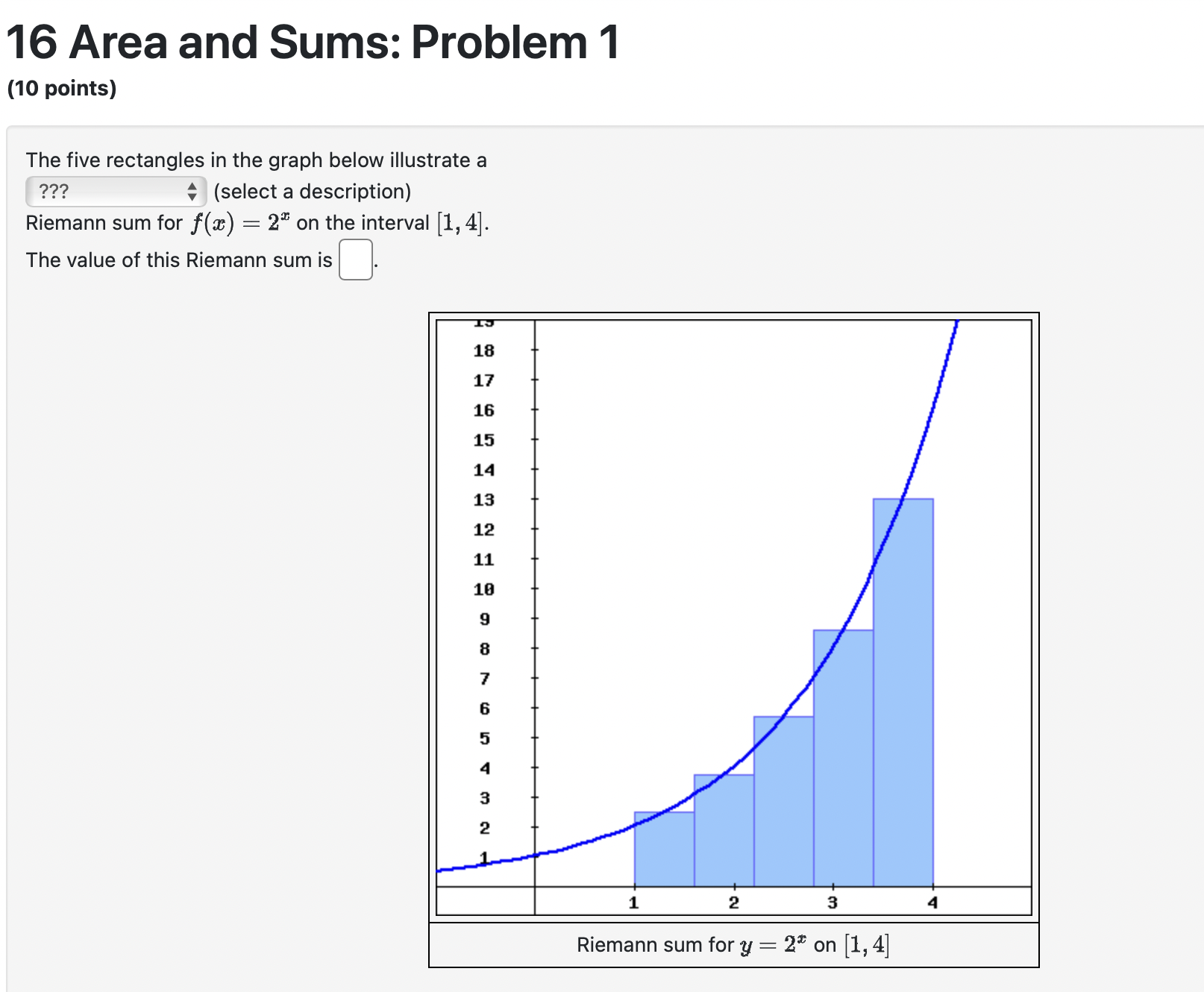
![sum for f(z) = 27 on the interval [1, 4]. The value](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67117b83063e0_97867117b82d1cef.jpg)

![3 2 Riemann sum for = 2% on [1, 4] a) The](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67117b83c8e08_97967117b8399835.jpg)

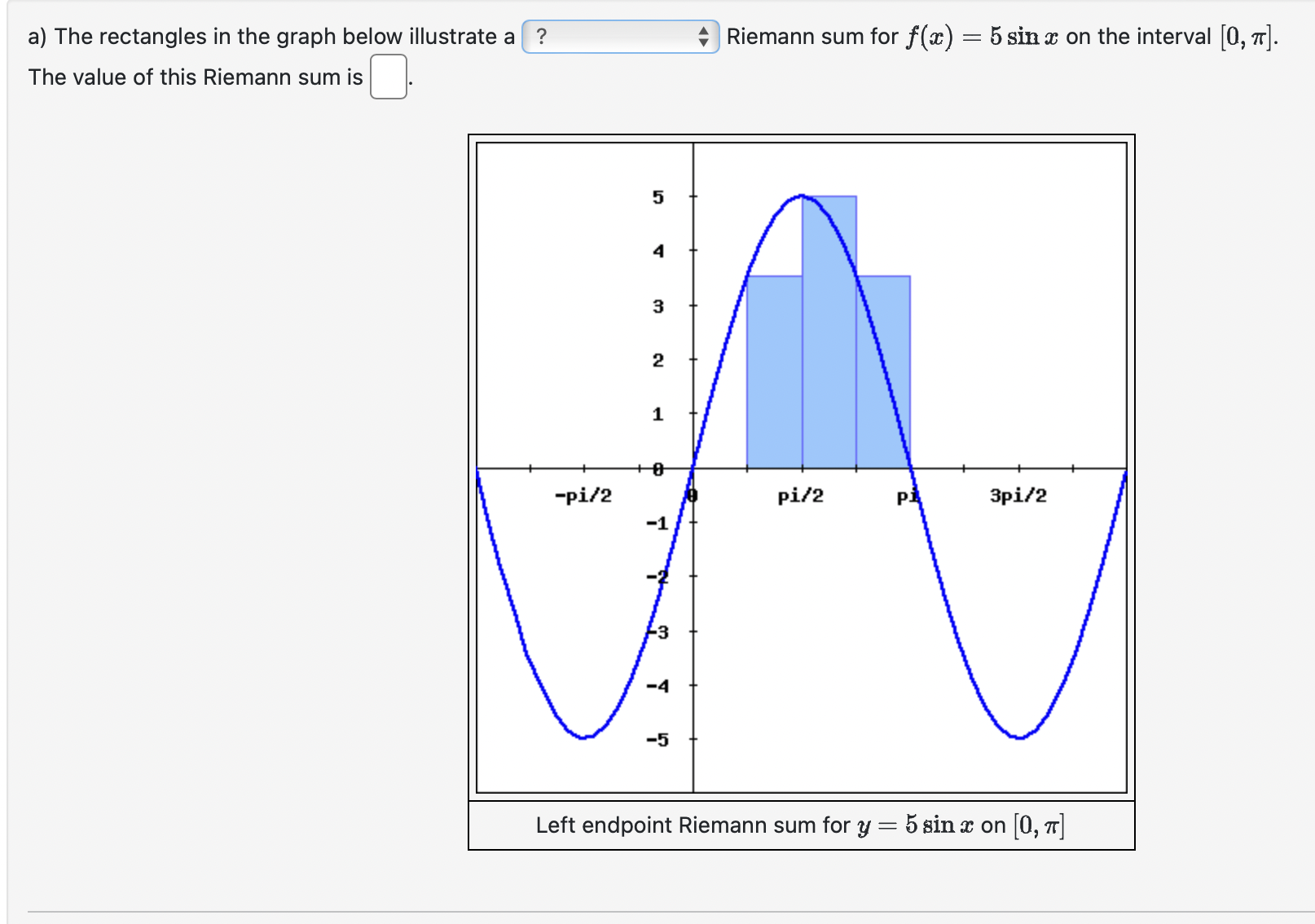
16 Area and Sums: Problem 1 (10 points) The five rectangles in the graph below illustrate a ??7? + (select a description) Riemann sum for f(z) = 27 on the interval [1, 4]. The value of this Riemann sum is | 9 8 7 6 5 4 3 2 Riemann sum for = 2% on [1, 4] a) The rectangles in the graph below illustrate a ? Riemann sum for f(a) = 5 sin x on the interval [0, 7]. The value of this Riemann sum is A No -pi/2 pi/2 pi 3pi/2 -1 -4 -5 Left endpoint Riemann sum for y = 5 sin x on [0, 7]b) The rectangles in the graph below illustrate a right endpoint . Riemann sum for f() = 5 sin a on the interval [0, 7]. The value of this Riemann sum is 4 ( V2 + 1) A + A -pi/2 pi/2 3pi/2 -1 -5 Right endpoint Riemann sum for y = 5 sin x on [0, 7]Estimate the area under the graph of f(:c) = % from = 1 to # = 5 by using 4 approximating rectangles. Estimate with right endpoints = Estimate with left endpoints = Compute the following Riemann sums of the function p(z) = 2% 4 1 on the interval 1 =z =4 Make an educated guess of the exact area bounded by p(z) = 2% + 1 and the z-axis on the interval [1, 4]. Exact Area = O Evaluate the sum: 250 k=50
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


