Question: 16. Let $V=operatorname{span}left{left(begin{array}{1}1 110111 Oend{array} ight), left(begin{array}{1}1 1 1end{array} ight), left(begin{array}{1}0 1111111 1end{array} ight) ight}$. a. Find all vectors $v in V^{perp}$ with length 1.

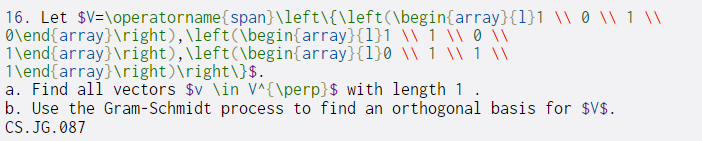
$16. Let $V=\operatorname{span}\left\{\left(\begin{array}{1}1 110111 O\end{array} ight), \left(\begin{array}{1}1 1 1\end{array} ight), \left(\begin{array}{1}0$

16. Let $V=\operatorname{span}\left\{\left(\begin{array}{1}1 110111 O\end{array} ight), \left(\begin{array}{1}1 1 1\end{array} ight), \left(\begin{array}{1}0 1111111 1\end{array} ight) ight\}$. a. Find all vectors $v \in V^{\perp}$ with length 1. b. Use the Gram-Schmidt process to find an orthogonal basis for $V$. CS.JG.087

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

16. Let $V=\operatornamespan}\left\{\left(\begin{array}{1}1 VON O\end{array} ight), \left(\begin{array}{1}1 WOW 1\end{array} ight), \left(\begin{array}{1}0 11 11 1\end{array} ight) ight\}$. a. Find...

16. Let $V=\operatorname [span]\left\{\left(\begin{array}{1}1 \\ 0 \\ 1 \\ 0\end{array} ight), \left(\begin{array} (1)1 \\ 1 \\ 0 \\ 1\end{array} ight), \left(\begin{array} {1}0 \\ 1 \\ 1 AV...

Use the information in Exhibit 24-5 to compute the expected volume variance at 780 units. Exhibit 24-5: Overhead Applied to Various Volumes Actual Productlon (In unlts) 600 700 800 Overhead appliled...

You are the Brand Executive of the dairy products department of Aarong. The company is planning to launch a low-fat yogurt for adults in December 2021 and you have the responsibility to apply the...

Family- friendly benefi ts may be attractive to staff but have disadvantages to employers. Select three of the benefi ts detailed in this chapter, list the disadvantages that may accompany...

Mullet Technologies is considering whether or not to refund a $75 million, 12 percent coupon 30-year bond issue that was sold 5 years ago. It is amortizing $5 million of flotation costs on the 12...

16. Let $V=\operatorname{span}\left\{\left(\begin{array}{1}1 110111 O\end{array} ight), \left(\begin{array}{1}1 1 1\end{array} ight), \left(\begin{array}{1}0 1111111 1\end{array} ight) ight\}$. a....

Determine the internal normal force, shear force, and moment at points F and E in the frame. The crate weighs 300lb. 1.5 | 1.5 ft 15 ft 15 A 0.4 ft 4 ft B.

For vectors i and , suppose ||u|| = 5, the angle between the vectors is 170 degrees, and the dot product u- = -8. Find the magnitude of vectori. Leave at least 4 decimals place. Don't round.

A bond is: multiple choice 1 a type of currency. a debt obligation. a type of bank. an equity obligation.

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

8. Compare and contrast the strengths and weaknesses of traditional training methods versus those of technology-based training methods.

6. Describe to a manager the different types of distance learning.

1. Explain how new technologies are influencing training.