Question: 16. Show that each conditional statement in Exercise 12 is a tautology by applying a chain of logical identities as in Example 8. (Do not

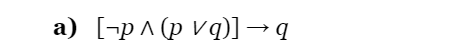
16. Show that each conditional statement in Exercise 12 is a tautology by applying a chain of logical identities as in Example 8. (Do not use truth tables.) a) [p(pq)]q EXAMPLE 8 how that (pq)(pq)

16. Show that each conditional statement in Exercise 12 is a tautology by applying a chain of logical identities as in Example 8. (Do not use truth tables.) a) [p(pq)]q EXAMPLE 8 how that (pq)(pq) is a tautology. Solution: To show that this statement is a tautology, we will use logical equivalences to demon strate that it is logically equivalent to T. (Note: This could also be done using a truth table.) (pq)(pq)(pq)(pq)(pq)(pq)(pp)(qq)TTTbyExample1andthecommutativebyExample3bythefirstDeMorganlawbytheassociativeandcommutativelawsfordisjunctionlawfordisjunction

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Show that the following conditional statement is a tautology by applying a chain of logical identities. (Do not use truth tables.) [p (p q)] q

PLEASE I NEED THE BEST OF THE BEST I DONT WANT TO FAIL AGAIN PLS DO (answer it all complete solution) I NEED PEFECT SCORE PLS PLS Complete the truth Table for the given statement by filling in the...

Please I need answer to these questions (11,12,13,14,15 and 16) thank you 9:09 LTEO 10. The values for the propositional variables p. g. s are determined as follows: p true q- false s true Determine...

Exercise 1.4.1: Proving tautologies and contradictions. About Show whether each logical expression is a tautology, contradiction or neither. (a) (p q) (q p) (b) (p q) (p q) (c) (p q) p (d) (p q) p...

Hello, I havetwo articles about S Corp. and C Corp., and IJUST need towrite a conclusion paragraph based on professor's questions. can you help me to write it? Articles are attached Accounting...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Quiz Instructions Select ALL that apply! Some questions may have multiple correct answers! Question 1 5 pts Determine which of the following sentences are logical statements :] Welcome to USF 3 If...

you bought as many whole shares of AMZN stock as you could with $2,596 at the Close price on the first trading day in the month of July each year from 2001 until 2010. How much were the shares owned...

The All-Power Gas and Electric Company cleared right of way across Larrys land and put up a power line, which it has maintained for the past 20 years. Now the company wants to replace the old line...

Signing of the contract by the two parties is A . not recorded until one or both parties perform under the contract. ( B . ) recorded at the time the contract is approved by both parties. C . not...

8:37 * N. 80% i ... OBJECTIVES: Create relationships Create a Pivot Table from Related Tables Create a PivotChart Modify the PivotChart The major section in this chapter :ontinuation is: Data...

=+2. Companies occasionally make mistakes that expose confidential information, such as when employees lose laptop computers containing

=+1. Why must you be careful when using information from the Internet in a business report? [LO-2]

=+5. Why are unsolicited proposals more challenging to write than solicited proposals? [LO-7]