Question: 1.6.2 Example: Poisson distribution Let Y1,., Yn be independent random variables each with the Poisson distri- bution f(y; 0) Yi = 0, 1, 2,

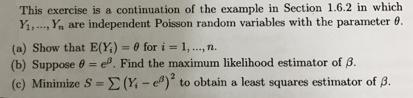
1.6.2 Example: Poisson distribution Let Y1,., Yn be independent random variables each

1.6.2 Example: Poisson distribution Let Y1,., Yn be independent random variables each with the Poisson distri- bution f(y; 0) Yi = 0, 1, 2, ... y!! with the same parameter 0. Their joint distribution is OYie-0 QYne-0 f (41,... ,Yn; 0) |[ S(4;;0) = ! Y2! Yn! i=1 . -no yn!y2!..yn! This is also the likelihood function L(0; y1,..., Yn). It is easier to use the log- likelihood function 1(0; Y1,. Yn) = log L(0; y1,..., Yn) = (E 4) log 0 no E(log y:!). ..... To find the maximum likelihood estimate 0, use dl . Yi - n. OP Equate this to zero to obtain the solution =E4i/n = J. Since de1/de? = -E4:/02 < 0, 1 has its maximum value when 0 = 6, con- firming that j is the maximum likelihood estimate.

Step by Step Solution

★★★★★

3.44 Rating (147 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To solve the given questions lets go through each part step by step Part a Show that EYi theta for i ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let X1,..., Xn be independent random variables with densities Prove that T = mini(Xi/i) is a sufficient statistic for Î¸. fx.(z0) = et6-7 I

Let X1,..., Xn be independent random variables with pdfs where Î¸ > 0. Find a two-dimensional sufficient statistic for Î¸. -(r otherwise Uz,10) =

Let X1, . . . be independent random variables with the common distribution function F, and suppose they are independent of N, a geometric random variable with parameter p. Let M = max(X1, . . . ,XN)....

Analyze the given picture as if you were a latent print examiner. You will see an impression with ridge events and features marked. You should: ?Identify the pattern. ?Determine what the indicated...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Statistics 149 Spring 2016 Assignment 1 Due Monday February 8, 2016 Homework is to be handed in either at the Monday lecture, or directly into the Stat 149 dropbox on the seventh oor of the Science...

SAMPLING MEAN: DEFINITION: The term sampling mean is a statistical term used to describe the properties of statistical distributions. In statistical terms, the sample mean from a group of...

Algorithms in Artificial Intelligence (or, the old name: Introduction to Algorithmic Decision Making) Part 1 Based on slides by David Sarne and Lirong Xia Course Tentative Schedule Introduction...

2 Maximum Likelihood Estimation [40 pts] This problem explores maximum likelihood estimation (MLE), which is a technique for estimating an unknown parameter of a probability distribution based on...

Hi, it's me again Thanks for helping me with the answer last time d u 1. (a) Let Y1, Y2, ..., Yn be a random sample from a Bernoulli (p) distribution (i.e. Binomial(1, p)). Show ELI K is a minimal...

What is the difference between a perpetual inventory and a physical inventory? If a company maintains a perpetual inventory, should its physical inventory at any date be equal to the amount indicated...

Horn Company accumulates the following adjustment data at December 31. Indicate (a) The type of adjustment (prepaid expense, accrued revenues and so on), and (b) The status of accounts before...

Cullumber Corp. had $ 7 3 0 , 0 0 0 net income in 2 0 2 5 . On January 1 , 2 0 2 5 , there were 2 0 0 , 0 0 0 shares of common stock outstanding. On April 1 , 2 3 , 4 0 0 shares were issued and on...

Russell Engineering provides consulting services related to land development. Below is the year-end adjusted trial balance of Russell Engineering. Required: Prepare an income statement, statement of...

King Company produces variations of its product, a megatron, in response to custom orders from its customers. On June 1, the company had no inventories of goods in process or finished goods but held...

Dye Corporation has fixed costs of $480,000. It has a unit selling price of $6, unit variable cost of $4.50, and a target net income of $1,500,000. Compute the required sales in units to achieve its...

Huang Companys break-even sales are $500,000. Assuming fixed costs are $180,000, what sales volume is needed to achieve a target net income of $90,000?

Define the term margin of safety. If Revere Company expects to sell 1,250 units of its product at $12 per unit, and break-even sales for the product are $13,200, what is the margin of safety ratio?

As presented in this chapter, Social Security a. taxes income up to about $160,000 per year (in 2023) at 12.4%. Beyond that amount, income is untaxed for Social Security. b. was designed to provide...

Suppose a random variable, x, follows a Poisson distribution. Let = 3 every day, find the P(X 12) over a week. Round answer to 4 decimal places. Answer: A bank gets an average of 12 customers per...

1. Geologists estimate the time since the most recent cooling of a mineral by counting the number of uranium fission tracks on the surface of the mineral. A certain mineral specimen is of such an age...

Question 14 options: Suppose a random variable, x, follows a Poisson distribution. Let = 3 every day, find the P(X 12) over a week. Round answer to 4 decimal places. Answer:

question 1: Suppose a random variable, x , arises from a binomial experiment. If n = 14, and p = 0.13, find the P(X = 3) using Excel. Round answer to 4 decimal places. Question 2: It is known that20%...

16 options: Suppose a random variable, x, follows a Poisson distribution. Let = 2.5 every minute, find the P(X 125) over an hour. Round answer to 4 decimal places

Suppose a random variable, x, follows a Poisson distribution. Let =2.5 every minute, find the P(X=125) over an hour. Round answer to 4 decimal places.