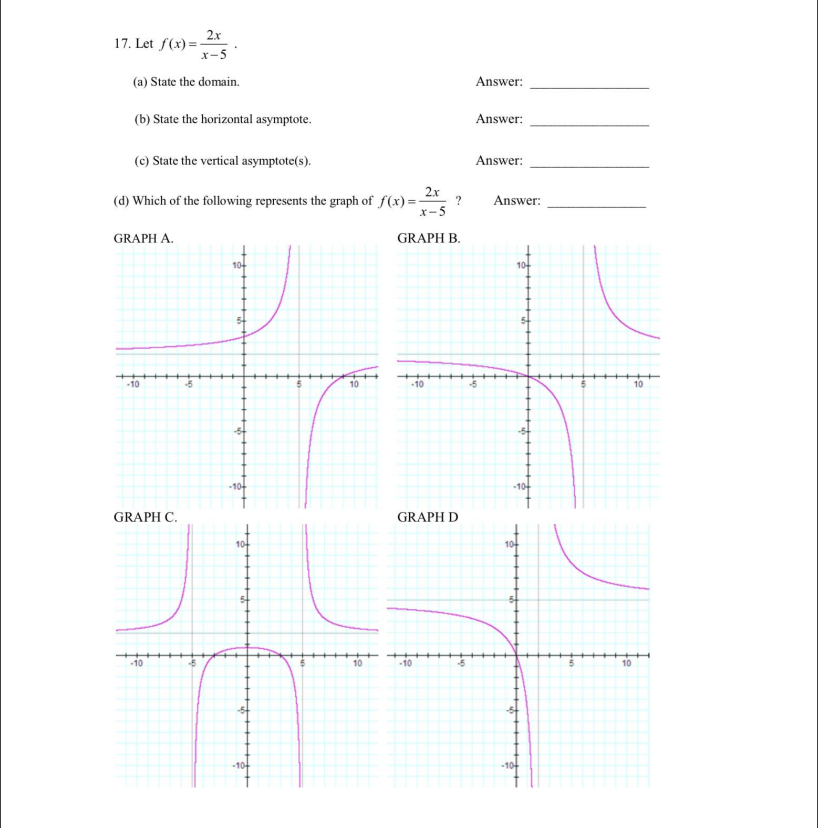
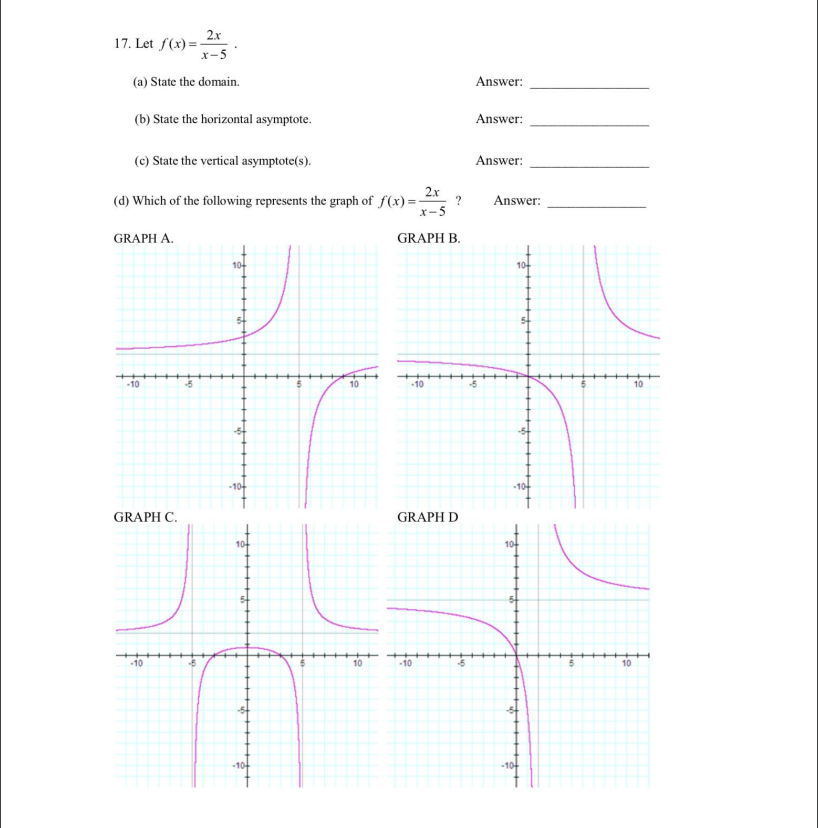
17. Let f(x) = 2x x-5 (a) State the domain. Answer: (b) State the horizontal asymptote. Answer: (c) State the vertical asymptote(s). Answer: (d) Which of the following represents the graph of f(x) = 4x ? Answer: x-5 GRAPH A. GRAPH B. 10 -10 10 -10- -104 GRAPH C. GRAPH D -10 10 10SHORT ANSWER, with work required to be shown, as indicated. 18. Find the equation for a line which passes through the points (-1, 9) and (-3, 1). Write the equation in slope-intercept form. Show work. 19. Find the exact solutions and simplify as much as possible: 2x3+ 15 = 14x. Show work. 20. Let f(x) = 3x2 - 15 and g(x) = x - 5. (a) Find the composite function (fog)(x) and simplify. Show work. (b) Find (f . g) (2). Show work. 21. A projectile is launched from a platform 18 feet high with an initial velocity of 104 feet per second, The height h of the projectile at / seconds after launch is given by h = -167 + 104 + 18 feet. (a) How many seconds after launch does the projectile attain maximum height? Show work. (b) What is the maximum height? Show work. 22. Solve: - x + 10 - + - 32 x+2 x2 - 4 - = 0. Show work. 23. Suppose that sin o = 4/5 and that O is a Quadrant II angle. (a) Find the exact value of cos 0. Show work. (b) Find the exact value of sin(20). Show work. 24. Prove the identity sec(x) (sin(x) + cos(x))" = sec(x) + 2 sin(x)