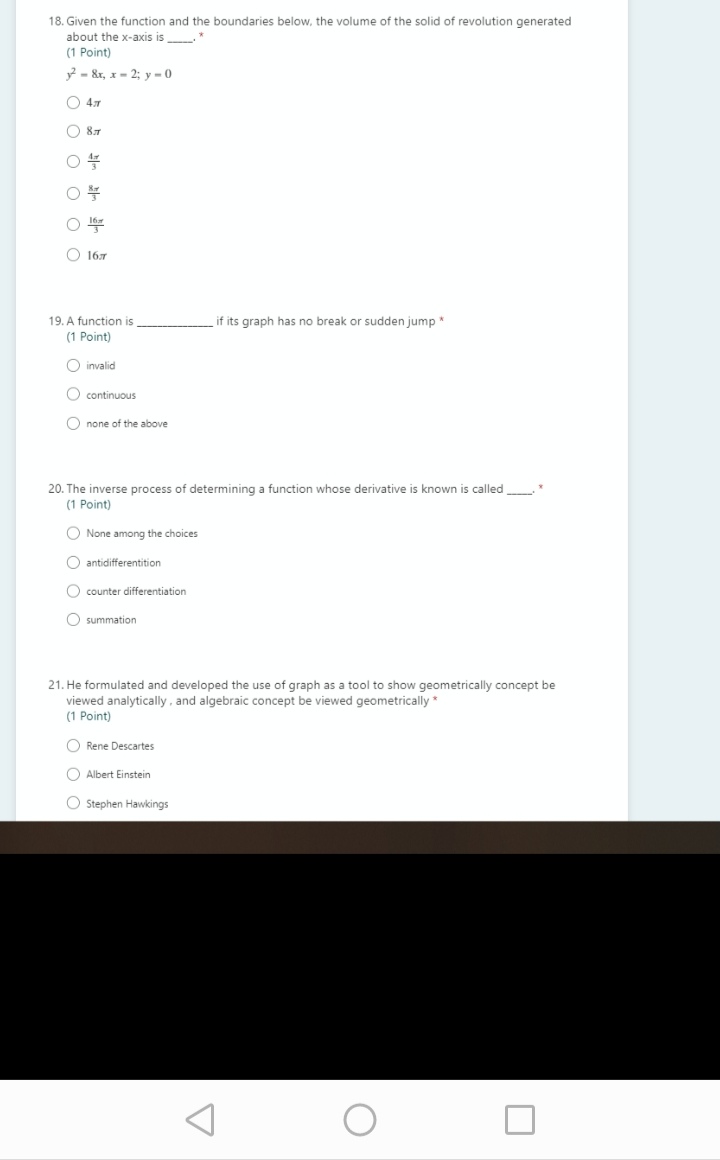
18. Given the function and the boundaries below, the volume of the solid of revolution generated about the x-axis is (1 Point) y - 8x, x - 2; y = 0 O 4x O 8 x 19. A function is if its graph has no break or sudden jump * (1 Point) O invalid O continuous O none of the above 20. The inverse process of determining a function whose derivative is known is called (1 Point) ONone among the choices O antidifferentition O counter differentiation summation 21. He formulated and developed the use of graph as a tool to show geometrically concept be viewed analytically , and algebraic concept be viewed geometrically * (1 Point) Rene Descartes Albert Einstein Stephen Hawkings O15. The domain is being referred to as the variable of function. * (1 Point) O dependent O independent arbitrary ONone of the above 16. The is defined by the equation f(x) = x * (1 Point) O inverse function O identity function irreversible function 17. is a rule of correspondence between two non-empty sets of elements called domain and range C (1 Point) O method of approximation function O Pythagorean Theorem O None of the above 18. Given the function and the boundaries below, the volume of the solid of revolution generated about the x-axis is (1 Point) y = &, x = 2; y = 0 O 4X11. The line that intersects a curve in two points is called a * (1 Point) O tangent line secant line cosine linte none of the above 12. An indeterminate function of algebraic and transcendental form ca be evaluated by (1 Point) so and O LHopital's rule O Newton's method of approximation O Tangential rule none of the above 13. The function that comes immediately after the symbol of integration is called the (1 Point) integrand variable of integration O constant of integration None among the choices 14. Which method of integration is teh counterpart of the the chain rule of differentiation? * (1 Point) integration by trigonometric identities O integration by substitution O integration by a particular function O integration by partial fractions O integration by partd