It was shown that the n-bit 2s complement integer B = b n 1 b n
Question:
It was shown that the n-bit 2’s complement integer B = bn−1bn−2 · · · b1b0 has the decimal value. 
. Based on this expression, multiplication of 2’s complement numbers, B × A, can be done by adding bi(A2i) to a partial product for i = 0 to n − 2 and subtracting bn−1(A2n−1) from the partial product.
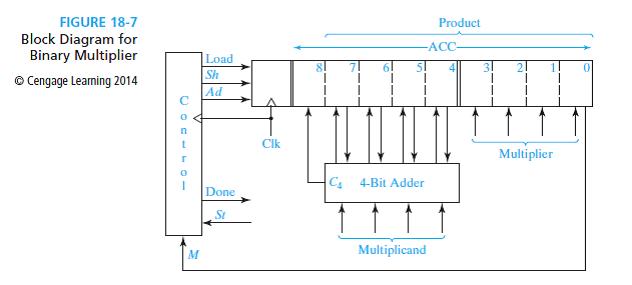
(a) Based on this algorithm, show the contents of ACC in Figure 18-7 for each step of the algorithm for the operands multiplicand A = 1101(−3) and multiplier B = 1010(−6). Repeat for operands A = 1000(−8) and B = 0110(6). Note that the value shifted into bit 7 of ACC will no longer be the carry-out from the adder as shown in Figure 18-7 (i.e., bit 8 of ACC will have to be replaced with a circuit that provides the proper value to shift into bit 7 of ACC).
(b) State in words what value should be shifted into bit 7 of ACC during a shift operation.
(c) Modify the circuit of Figure 18-7 so that 2’s complement numbers can be multiplied using this algorithm. Replace bit 8 of ACC with a circuit that provides the value to shift into bit 7 of ACC during a shift operation. Let M3 be the sign bit of the multiplicand. Let Su be the control signal from the controller when a Subtract operation is required.
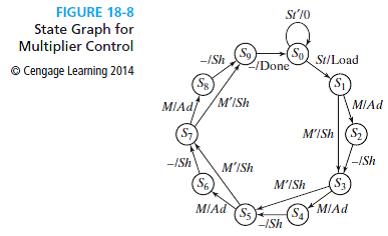
(d) Using the modified circuit of part (c), modify the state graph of Figure 18-8 to perform 2’s complement multiplication.
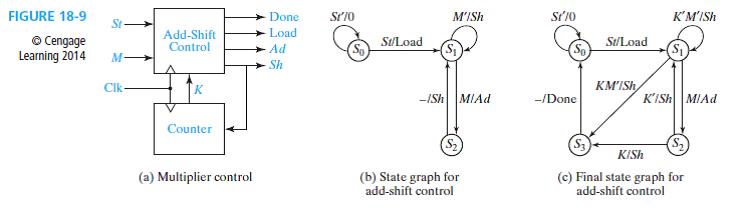
(e) Using the modified circuit of part (c), modify the state graph of Figure 18-9(c) to perform 2’s complement multiplication.
Expert Answer:
a To demonstrate the contents of ACC for each step of the algorithm well consider two examples A 1101 3 and B 1010 6 and A 1000 8 and B 0110 6 For A 1... View the full answer
