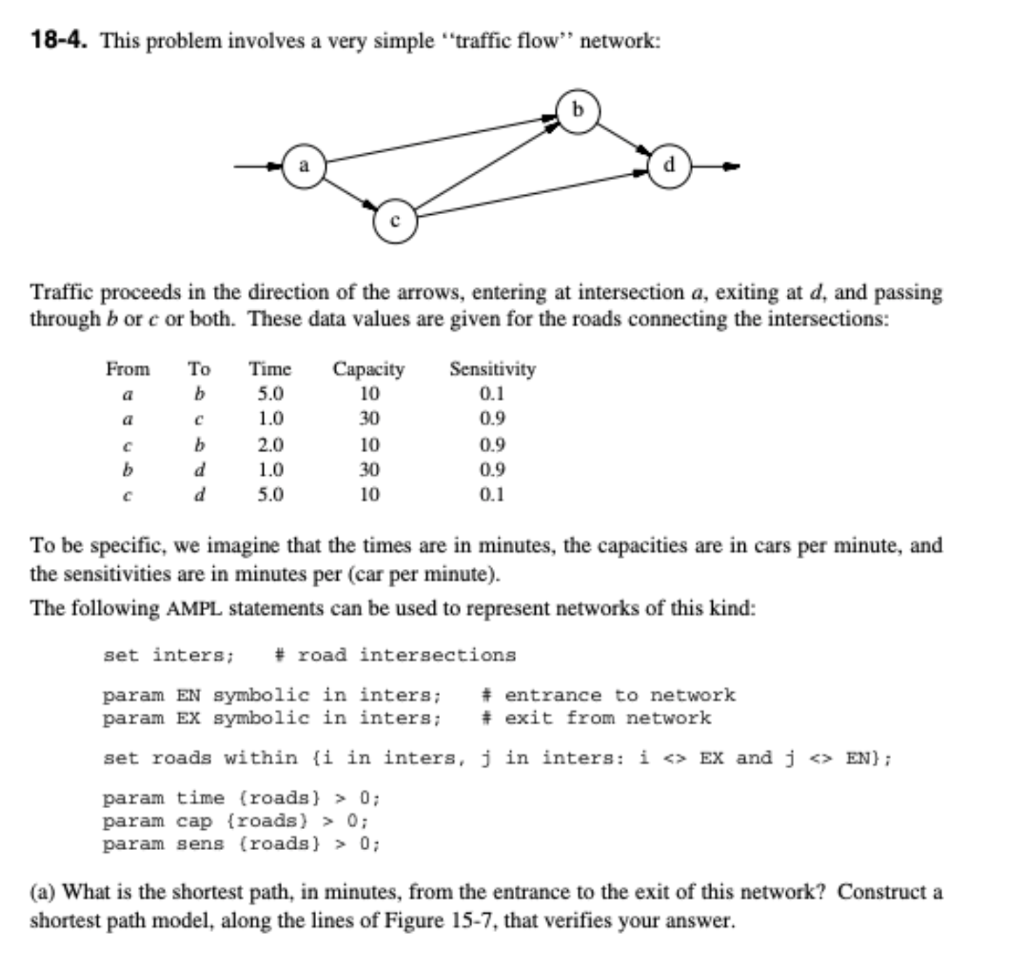
18-4. This problem involves a very simple traffic flow network: d Traffic proceeds in the direction of the arrows, entering at intersection a, exiting at d, and passing through bor e or both. These data values are given for the roads connecting the intersections: From Time Capacity Sensitivity b To a 5.0 a c b b d d 1.0 2.0 1.0 5.0 10 30 10 30 10 0.1 0.9 0.9 0.9 0.1 To be specific, we imagine that the times are in minutes, the capacities are in cars per minute, and the sensitivities are in minutes per (car per minute). The following AMPL statements can be used to represent networks of this kind: set inters; # road intersections param EN symbolic in inters; # entrance to network param Ex symbolic in inters; # exit from network set roads within {i in inters, j in inters: i Ex and j EN); param time (roads) > 0; param cap {roads) > 0; param sens (roads) > 0; (a) What is the shortest path, in minutes, from the entrance to the exit of this network? Construct a shortest path model, along the lines of Figure 15-7, that verifies your answer. 18-4. This problem involves a very simple traffic flow network: d Traffic proceeds in the direction of the arrows, entering at intersection a, exiting at d, and passing through bor e or both. These data values are given for the roads connecting the intersections: From Time Capacity Sensitivity b To a 5.0 a c b b d d 1.0 2.0 1.0 5.0 10 30 10 30 10 0.1 0.9 0.9 0.9 0.1 To be specific, we imagine that the times are in minutes, the capacities are in cars per minute, and the sensitivities are in minutes per (car per minute). The following AMPL statements can be used to represent networks of this kind: set inters; # road intersections param EN symbolic in inters; # entrance to network param Ex symbolic in inters; # exit from network set roads within {i in inters, j in inters: i Ex and j EN); param time (roads) > 0; param cap {roads) > 0; param sens (roads) > 0; (a) What is the shortest path, in minutes, from the entrance to the exit of this network? Construct a shortest path model, along the lines of Figure 15-7, that verifies your