1(a) Eliminate the parameter = ??2(a) Graph the paths of both particles... = ??2(b) Find the collision... = ??2(c) = ??

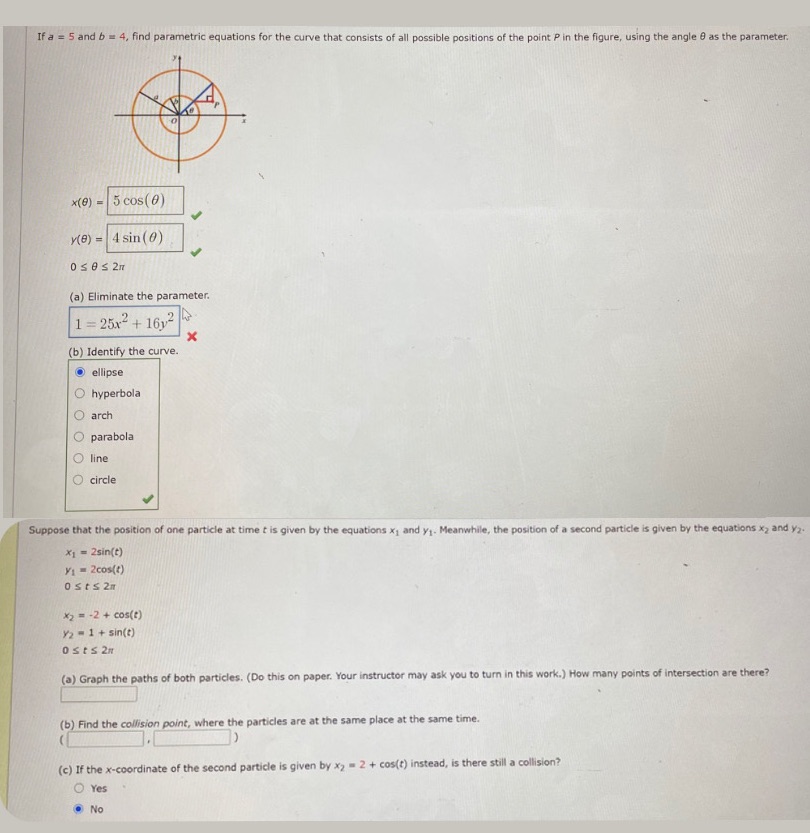
If a = 5 and b = 4, find parametric equations for the curve that consists of all possible positions of the point P in the figure, using the angle 0 as the parameter. x(0) = 5 cos(0) v(8) = 4 sin(0) (a) Eliminate the parameter. 1 =25x- + 1624 (b) Identify the curve. O ellipse O hyperbola O arch O parabola O line O circle Suppose that the position of one particle at time t is given by the equations x, and y1. Meanwhile, the position of a second particle is given by the equations x, and yz. X1 = 2sin(t) 1 = 2cos(() Osts 2n *2 = -2 + cos(t) y2 = 1 + sin(t) OSts 20 (a) Graph the paths of both particles. (Do this on paper. Your instructor may ask you to turn in this work.) How many points of intersection are there? (b) Find the collision point, where the particles are at the same place at the same time. (c) If the x-coordinate of the second particle is given by x2 = 2 + cos(f) instead, is there still a collision? O Yes No