1.Evaluate each integral by making an appropriate substitution.

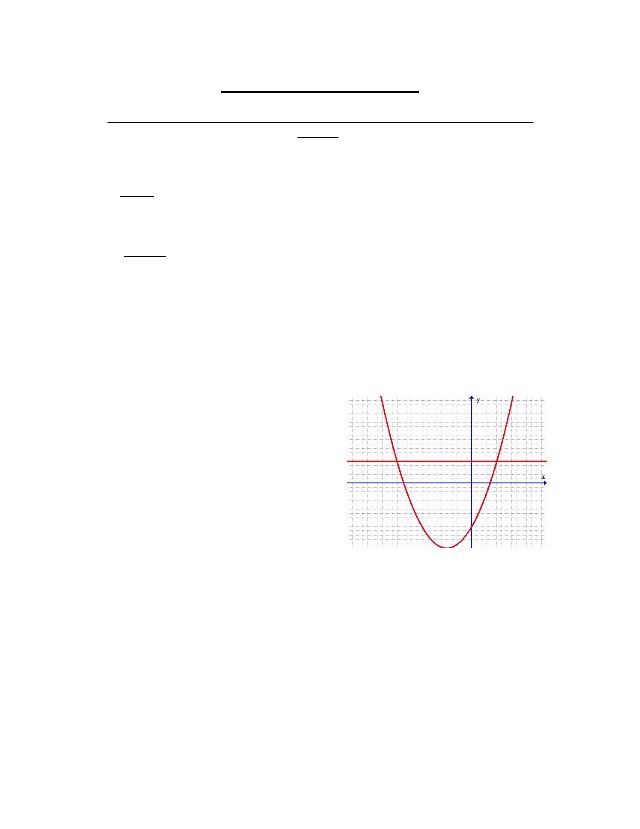
2.Find the area of the region bounded above by the graph ofand below by the graph of

3.LetRbe the closed region between the graphs of andon the interval [0, 1]. Find the volumeVof the solid obtained by revolvingRabout thex-axis.

4.LetRbe the closed region between the graphs of andon the interval [0, 1]. Find the volumeVof the solid obtained by revolvingRabout they-axis. (Same graph as for Problem3)

5.Find thelength of arcon the graph of

6.Find thearea of the surfacegenerated by revolving about thex-axis the curve

7.Fill in the values ofandfor . Provide detail to support your answers.

8.Calculate the derivative for

9.Use the definition of an improper integral to evaluate the followingintegrals. If an integral converges, evaluate its value.

10.Using the indicated techniques to evaluate the following integrals. Show work detail to support your solutions.Solving using other methods or with no detail is not acceptable.

11.Complete the square in the denominator, make appropriate substitution, and integrate.

12.Find the partial fraction decomposition for the rational functionand then evaluate the integral

13.State whether the sequence converges or diverges. If it converges, find itslimit.

14.Using theIntegral Testto test the following series for convergence.Solving using other methods or with no detail is not acceptable.

15.Determine whether the following series converge or diverge.Indicate the test you use.

16.Determine whether the seriesconverges or diverges. If it converges, find itssum.

17.Determine whether the seriesconverges conditionally, or converges absolutely, or diverges and give reasons for your conclusions.

18.Find theinterval of convergencefor the power series

19.Use substitution method and a known power series to find power series for .Please express your answer inonesigma notation.

Math 141 Final Exam (An answer, even if \"correct\" but lacking work, will NOT receive full credit!) 1. Evaluate each integral by making an appropriate substitution. (a) x x 2 4 dx (b) e x e x 0 e x e x dx 1 (c) tan x sec 4 xdx 2. Find the area of the region bounded above by the graph of graph of 2 f ( x) x 2 x 2 . g ( x) 1 and below by the 3. Let R be the closed region between the graphs of and on the interval y 2 x y 2 x [0, 1]. Find the volume V of the solid obtained by revolving R about the x- axis. 2 4. Let R be the closed region between the graphs of and y 2 x on the interval y 2 x [0, 1]. Find the volume V of the solid obtained by revolving R about the y- axis. (Same graph as for Problem3) 5. Find the length of arc on the graph of from x 1 to 2 f ( x) x 3 / 2 3 x 4 6. Find the area of the surface generated by revolving about the x-axis the curve on . [0,2] 1 3 f ( x) x 3 ' 7. Fill in the values of f 1 ( x ) and ( f 1) (x ) for support your answers. x f (x) 1 2 3 2 3 1 ' f (x ) 5 1 x=1, 2,3 . Provide detail to ' 1 f (x ) ( f 1) (x ) 3 8. Calculate the derivative for y arctan( x 2 1) 9. Use the definition of an improper integral to evaluate the following integrals. If an integral converges, evaluate its value. (a) 1 1 0 x 0.9 dx 3 (b) x 1 2x dx 1 2 10. Using the indicated techniques to evaluate the following integrals. Show work detail to support your solutions. Solving using other methods or with no detail is not acceptable. (a) (Trigonometric substitution) dx 1 4x (b) 2 (Trigonometric substitution) x2 16 x2 dx (c) (Integration by Parts) x 2 ln xdx 11. Complete the square in the denominator, make appropriate substitution, and integrate. 1 x 2 6 x 10dx 12. Find the partial fraction decomposition for the rational function then evaluate the integral 5 (u 2)(u 3) and 5 (u 2)(u 3)du 13. State whether the sequence converges or diverges. If it converges, find its limit. ( n 3) 2 n 2 , n 1,2, n 4 14. Using the Integral Test to test the following series for convergence. Solving using other methods or with no detail is not acceptable. 1 2 n 3 n(ln n) 5 15. Determine whether the following series converge or diverge. Indicate the test you use. (a) 1 sin 2 k k 2 k1 (b) n n 1 3 4n 1 2n 2 2 16. Determine whether the series converges or diverges. If it 1 n 3 n n 0 3 4 converges, find its sum. 17. Determine whether the series converges conditionally, or converges ( 1) n n 0 n 3 absolutely, or diverges and give reasons for your conclusions. 18. Find the interval of convergence for the power series 1 xn n 0 n 2 19. Use substitution method and a known power series to find power series for Please express your answer in one sigma notation. 6 e3x 1 x