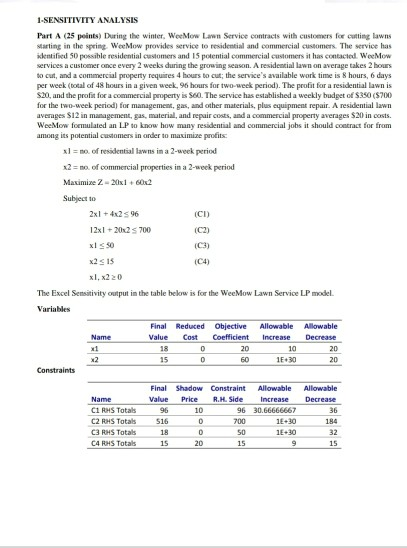
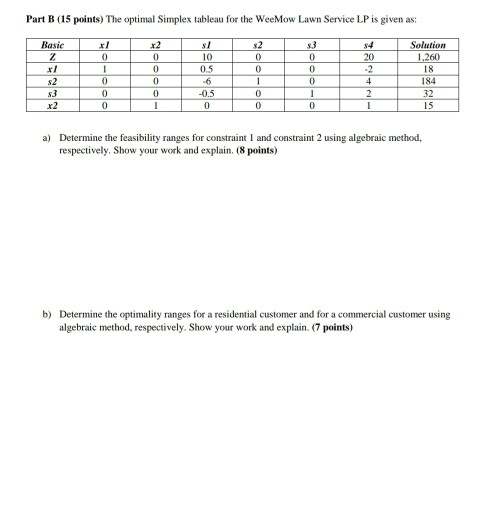
1-SENSITIVITY ANALYSIS Part A (25 points) During the winter. WeeMow Lawn Service contracts with customers for cutting lawns Starting in the spring WeeMow provides service to residential and commercial customers. The service has identified 50 possible residential customers and 15 potential commercial customers it has contacted. WeeMow services a customer once every 2 weeks during the growing season. A residential lawn on average takes 2 hours to cut, and a commercial property requires 4 hours to cut; the services available work time is 8 hours, 6 days per week (total of 48 hours in a given week, 96 hours for two-week period). The profit for a residential lawn is $20, and the profit for a commercial property is S60. The service has established a weekly budget of $350 (5700 for the two-week period for management, gas, and other materials, plus equipment repair. A residential lawn averages $12 in management, gas, material, and repair costs, and a commercial property averages $20 in costs. WeeMow formulated an LP to know how many residential and commercial jobs it should contract for from among its potential customers in order to maximize profits: x1 = no. of residential lawns in a 2-week period x2 = no. of commercial properties in a 2-week period Maximize 2-20x160x2 Subject to 2x1 + 4x2 5 96 (CI) 12x120x2 5 700 (C2) xl 50 (C3) 2515 (C4) xl, x220 The Excel Sensitivity output in the table below is for the Wee Mow Lawn Service LP model Variables Final Reduced Objective Allowable Allowable Name Value Cost Coefficient Increase Decrease x1 20 20 15 60 1E30 20 Constraints Final Shadow Constraint Allowable Allowable Name Value Price R.H. Side Increase Decrease CI RHS Totals 10 96 30.66666667 36 C2 RHS Totals 516 0 1E+30 184 C3 RHS Totals 18 50 15.30 C4 RHS Totals 15 15 18 10 D 0 96 700 32 D 20 15 9 a) Determine the objective function value and the optimum solution to the model from the above Excel Sensitivity output. (5 points) b) If you are able to increase the level of the restrictions (constraint RHS's) in LP model, which constraint(s) do you consider to change? Why? (5 points) c) If WeeMow could increase its two-week budget by $1, or increase its total available work time by 1 hour, which would be more profitable? (5 points) d) Determine the new objective function value in case WeeMow Lawn Service were able to identify 20 potential commercial customers instead of 15. Explain. (5 points) e) Determine the new objective function value if the profit for a residential lawn is increased from 20 to 30? Explain. (5 points) Part B (15 points) The optimal Simplex tableau for the WeeMow Lawn Service LP is given as: 1 0 Basic Z 1 s2 53 x2 x2 0 0 0 0 - Solution 1.260 18 sl 10 0.5 -6 -0.5 0 33 0 0 0 34 20 -2 4 2 0 0 1 0 0 0 0 0 184 32 15 1 0 - a) Determine the feasibility ranges for constraint 1 and constraint 2 using algebraic method, respectively. Show your work and explain. (8 points) b) Determine the optimality ranges for a residential customer and for a commercial customer using algebraic method, respectively. Show your work and explain. (7 points)