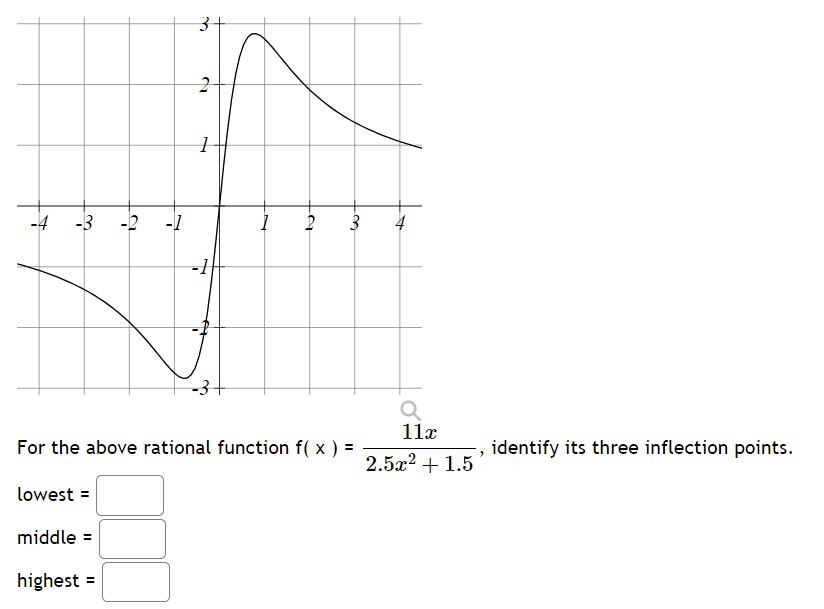
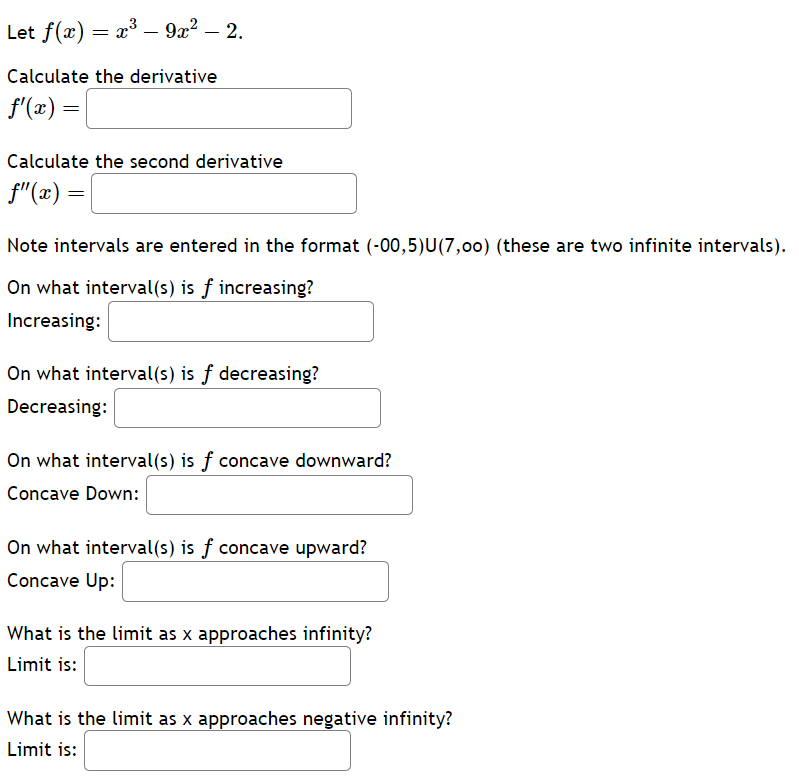
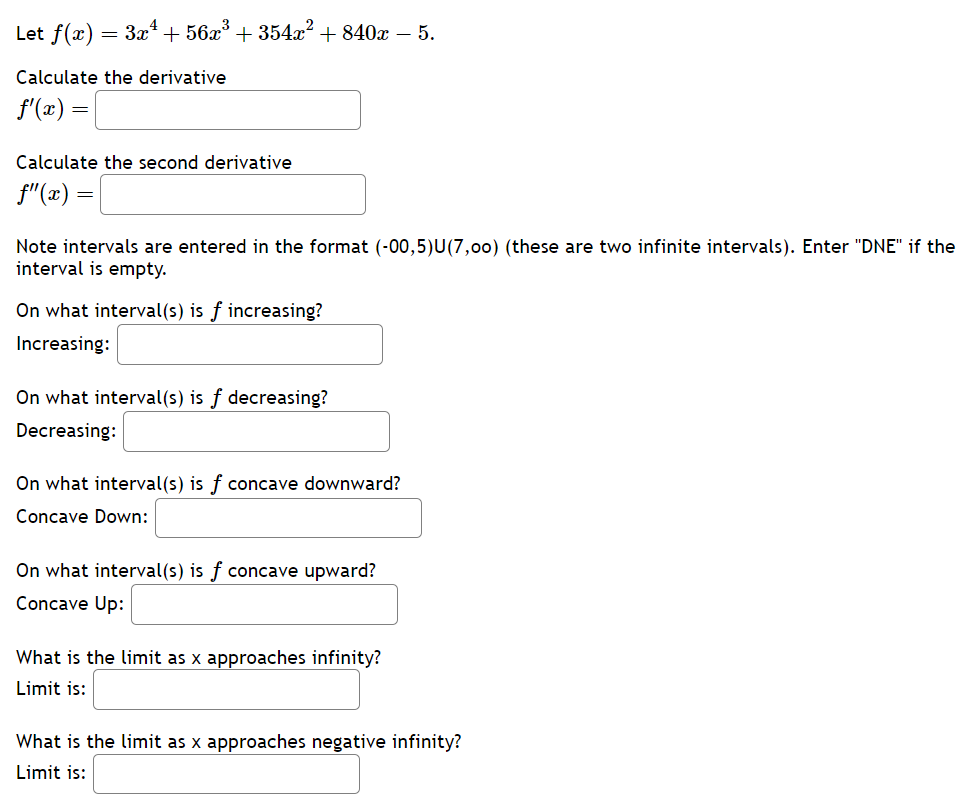
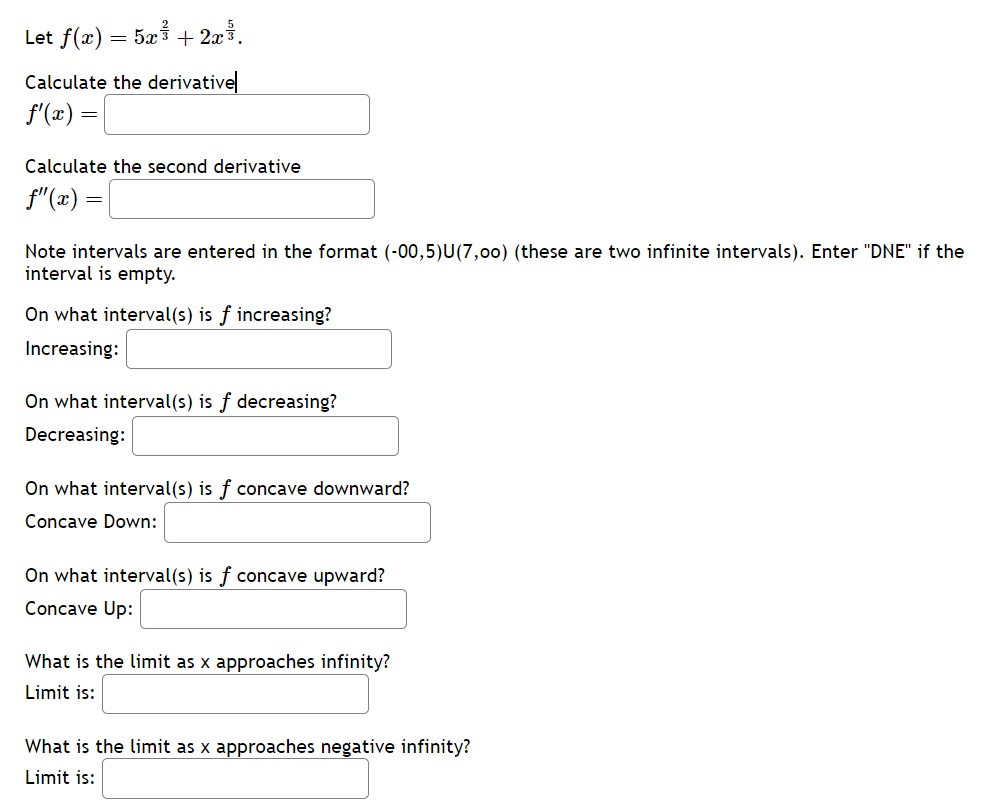
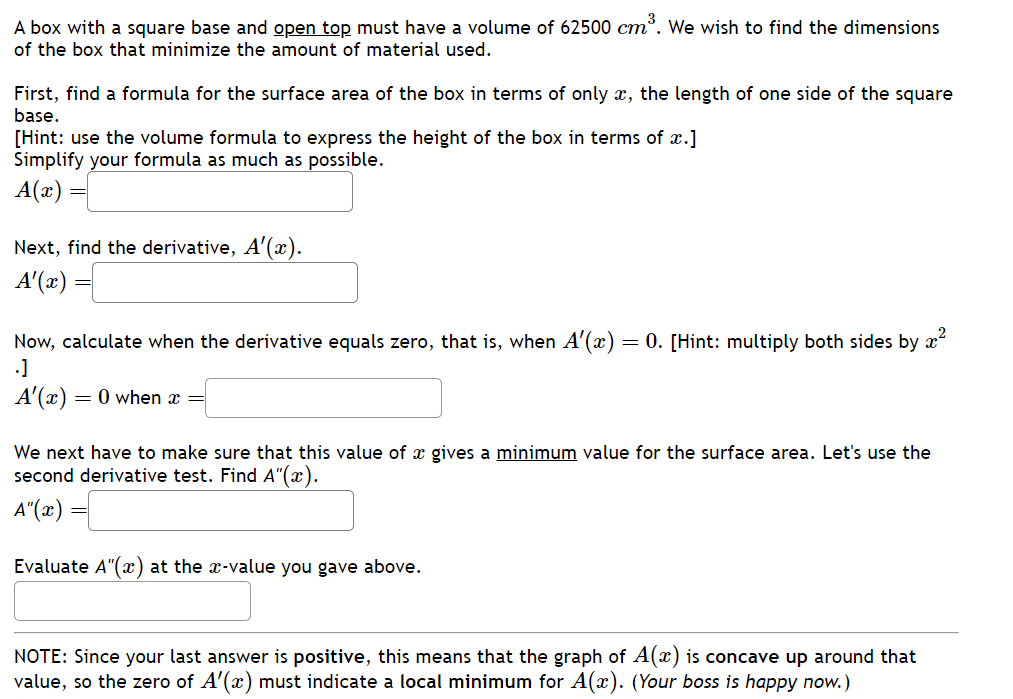
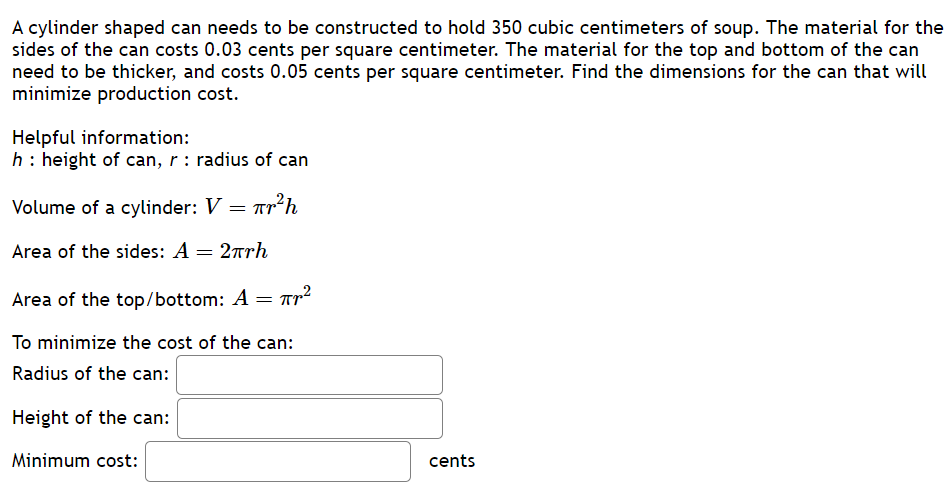
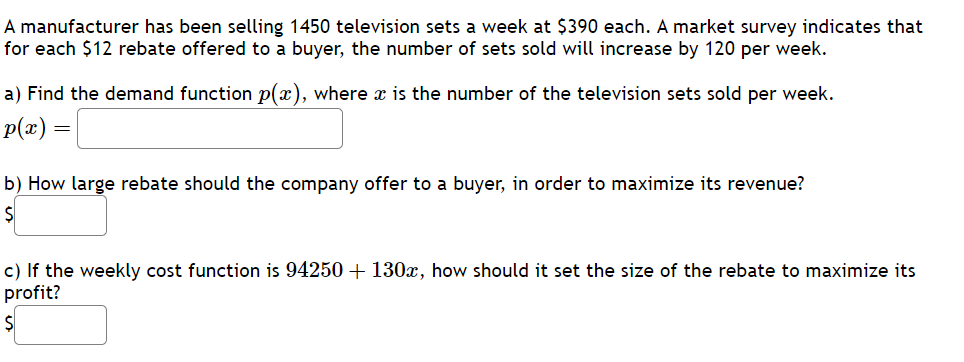
2 -1 -3 . . 11z . L . . . For the above rational function f( x ) = , identify its three inflection points. f ' 25224+ 1.5 lowest = ' middle = \\ | highest = r Let f(z) = z 922 2. Calculatg the derivative \\ fl(z) =| | Calculate'the second derivative ' () =| | MNote intervals are entered in the format (-00,5)U(7,00) (these are two infinite intervals). On what interval(s) is f increasing? Increasing: ' ' On what interval(s) is f decreasing? Decreasing: ' ' On what interval(s) is f concave downward? Concave Down: ' ' On what interval(s) is f concave upward? Concave Up: ' ' What is the limit as x approaches infinity? Limit is: \\ \\ What is the limit as x approaches negative infinity? Limit is: ' \\ Let f(z) = 3z* + 562 + 3542% + 840z 5. Calculate the derivative fle) = | Calculate)the second derivative f'(z) =| | Note intervals are entered in the format (-00,5)U(7,00) (these are two infinite intervals). Enter "DNE" if the interval is empty. On what interval(s) is f increasing? Increasing: ' ' On what interval(s) is f decreasing? Decreasing: ' ' On what interval(s) is f concave downward? Concave Down: ' ' On what interval(s) is f concave upward? Concave Up: ' ' What is the limit as x approaches infinity? Limit is:| | What is the limit as x approaches negative infinity? Limit is: | | Let f(x) = 5as + 2. Calculate the derivative] \\ f(z) =| | Calculate)the second derivative ' f(z) = ' ' MNote intervals are entered in the format (-00,5)U(7,00) (these are two infinite intervals). Enter "DNE" if the interval is empty. On what interval(s) is f increasing? Increasing: ' | On what interval(s) is f decreasing? Decreasing: | ' On what interval(s) is f concave downward? Concave Down: ' ' On what interval(s) is f concave upward? Concave Up: ' | What is the limit as x approaches infinij:y? Limit is: \\ \\ What is the limit as x approaches negative infinity? Limit is: \\ \\ A box with a square base and open top must have a volume of 62500 cm?>. We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only &, the length of one side of the square base. [Hint: use the volume formula to express the height of the box in terms of x.] Simplify your formula as much as possible. A(z) =\\' J Next, find the derivative, A'(z). Allz) = | Now, calculate when the derivative equals zero, that is, when A'(x) = 0. [Hint: multiply both sides by z? -] A'(z) = 0whenz = We next have to make sure that this value of x gives a minimum value for the surface area. Let's use the second derivative test. Find A"(x). #l) = | Evaluate A"(z) at the z-value you gave above. NOTE: Since your last answer is positive, this means that the graph of A[;r:) is concave up around that value, so the zero of A'(z) must indicate a local minimum for A(z). (Your boss is happy now.) A rancher wants to fence in an area of 1,000,000 square feet in a rectangular field and then divide it in half with a fence down the middle parallel to one side. What is the shortest length of fence that the rancher can use? A cylinder shaped can needs to be constructed to hold 350 cubic centimeters of soup. The material for the sides of the can costs 0.03 cents per square centimeter. The material for the top and bottom of the can need to be thicker, and costs 0.05 cents per square centimeter. Find the dimensions for the can that will minimize production cost. Helpful information: h : height of can, r : radius of can Volume of a cylinder: V = nr'h Area of the sides: A = 2nrh Area of the top/bottom: A = 7r? To minimize the cost of the can: Radius of the can: ' ' Height of the can: | ' Minimum cost: | ' cents A farmer finds that if she plants 100 trees per acre, each tree will yield 80 bushels of fruit. She estimates that for each additional tree planted per acre, the yield of each tree will decrease by 3 bushels. How mai trees should she plant per acre to maximize her harvest? trees Give your answer rounded to the nearest whole number. A manufacturer has been selling 1450 television sets a week at $390 each. A market survey indicates that for each 512 rebate offered to a buyer, the number of sets sold will increase by 120 per week. a) Find the demand function p(:r:), where x is the number of the television sets sold per week. p(z) = \\ \\ b) How large rebate should the company offer te a buyer, in order to maximize its revenue? I c) If the weekly cost function is 94250 + 130z, how should it set the size of the rebate to maximize its profit? % | I piece of cardboard measuring 12 inches by 14 inches is formed into an open-top box by cutting squares with side length x from each corner and folding up the sides. Find a formula for the volume of the box in terms of = V(z) = \\: :\\ Find the value for = that will maximize the volume of the box ==| |