Question: (a) Show geometrically that the set S = {(r1, 2) E R? : r1 2.x2 > 2} is convex. (b) Prove algebraically that the

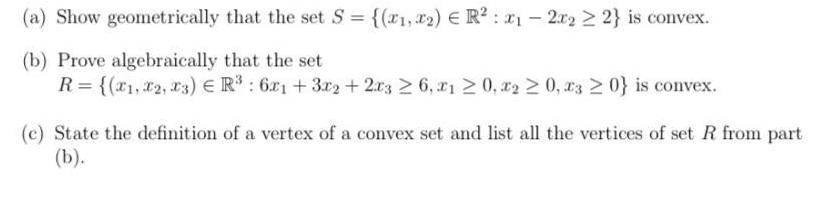
(a) Show geometrically that the set S = {(r1, 2) E R?

(a) Show geometrically that the set S = {(r1, 2) E R? : r1 2.x2 > 2} is convex. (b) Prove algebraically that the set R= {(x1, x2, x3) ER : 6x1 + 3r2+ 2x3 2 6, r1 20, r2 2 0, x3 2 0} is convex. (c) State the definition of a vertex of a convex set and list all the vertices of set R from part (b).

Step by Step Solution

★★★★★

3.51 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Definition Lets first recall the definition of a convex function Definition 1 A function f R n R is ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

6362853bc759b_236834.pdf

180 KBs PDF File

6362853bc759b_236834.docx

120 KBs Word File

Students Have Also Explored These Related Mathematics Questions!

The linear system x1 + 1/2 x2 + 1/3 x3 = 5/6, 1/2 x1 + 1/3 x2 + 1/4 x3 = 5/12, 1/3 x1 + 1/4 x2 + 1/5 x3 = 17/60

Prove Theorem 5.5.13; that is, show that a. Set e = |x - | and show that if x > , then P(Xn x) > P(|Xn - | ). Deduce the => implication. b. Use the fact that {x : |x - >} = {x : x - . } to deduce...

Prove Theorem 8.10. Theorem 8.10 If X1 and X2 are independent random variables, X1 has a chi-square distribution with v1 degrees of freedom, and X1 + X2 has a chi-square distribution with v > v1...

Figure shows a section of a circuit. The resistances are R 1 = 2.0?, R 2 = 4.0?, and R 3 = 6.0?, and the indicated current is i = 6.0 A. The electric potential difference between points A and B that...

In Figure 18.10, assume that the link between R1 and R2 is upgraded to 170 kbps and the link between the source host and R1 is now downgraded to 140 kbps. What is the throughput between the source...

(a) Redesign the circuit shown in Figure P5.49 using $V_{C C}=9 \mathrm{~V}$ such that the voltage drop across $R_{C}$ is $\left(\frac{1}{3} ight) V_{C C}$ and the voltage drop across $R_{E}$...

Kiss example with two distinct observations In this problem we use the same setup as the previous question. For the next three questions, assume that the two observations R1 and R2 and are different....

Assume that X ~ B(1, 0) is observed, and that it is desired to estimate 0 [0, 1]under squared-error loss. Since the loss is convex, attention can be restricted to nonrandomized decision rules. A...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

Graphics Describe a quad-tree encoding method for greyscale images. [6 marks] Given the following greyscale image, draw a diagram showing how it would be encoded using your method from the previous...

Real life example diversification bias and empathy gap?

What is the highest court in the United States? What is its jurisdiction? Where does it hear cases?

What assumption is made if the statement break even units is 5 4 units is made? Question 3 options: 1 ) if the company sells 5 5 units they aren't making a profit 2 ) if the company sells 5 4 units...

Block A and block B are connected by a massless string over a smooth and massless pulley as shown below. The masses of block A and block Il are 2 kg and I kg respectively. The two blocks are released...

Two children sitting on a sled at rest in the snow ask you to pull them. You oblige by pulling on the sled's rope, which makes an angle of 40 with the horizontal (Figure 5- 7). The children have a...

Three people flip coins. If one person has a different face showing from the other two, that person loses and the game is over. Find the probabitlity that the number of turns taken to determine the...

Use algebraic manipulation to show that for three input variables x 1 , x 2 , x 3 for m(1,2,3,4,5,6,7)= x 1+ x 2 +x 3

In 2015, David, age 65, had adjusted gross income of $32,000. During the year he paid the following medical expenses: Prescription medicines $200 Doctors $2,500 Medical care insurance $400...

The "Swiss Cheese" model of human error describes three levels of human failure. Question 4 options: True False

c) In a model of compensating wage differentials the indifference curves of "risk lovers" are steeper than those of risk-averse workers.10. What is Lewis's explanation for rural-urban migration? Why...

statistics and probability 3 Problem 1 (40p) (Well-behaved preferences) Lila spends her income on two goods: food, x1; and clothing, x2. a) The price food is p1= 2 and one piece of clothing costs p2=...

Problem 1 (40p) (Well-behaved preferences) Lila spends her income on two goods: food, 21, and clothing. 12. a) The price food is p1= 4 and one piece of clothing costs p2= 8 . Show geometrically...

MA 313/513 Menu 1 Directions You are required to complete eight of the main menu items: 6 required (Cowpens, Bullpens, Increasing Pattern #3, Robbie the Robot, Increasing Pattern #1, Polygon...

1. The following question refers to a model of imperfect monopsonistic wage discrimination against females like the one presented in class. a) Indicate how imperfect monopsonistic wage discrimination...