Question: 2 4 . 1 0 The temperature distribution in a tapered conical cooling fin ( Fig . P 2 4 . 1 0 ) is
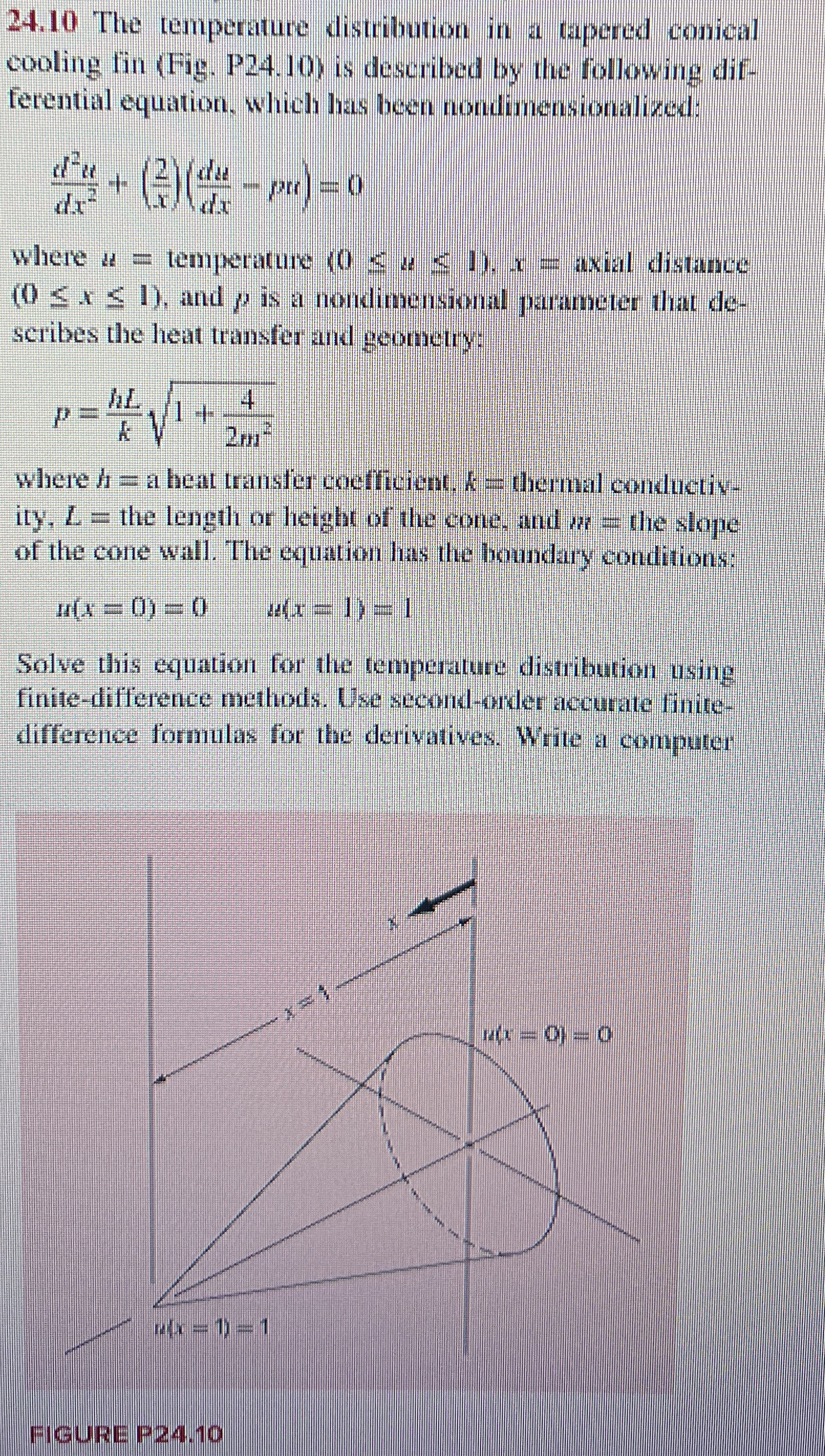
The temperature distribution in a tapered conical cooling fin Fig P is described by the following differential equation, which has been nondimensionalized:
where temperature axial distance and is a nondimensional parameter that describes the heat transfer and geometry:
where a heat transfer coefficient, thermal conductivity, the length or height of the cone, and the slope of the cone wall. The equation has the boundary conditions:
Solve this equation for the temperature distribution using finitedifference methods. Use secondorder accurate finitedifference formulas for the derivatives. Write a computer
FIGURE P
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


