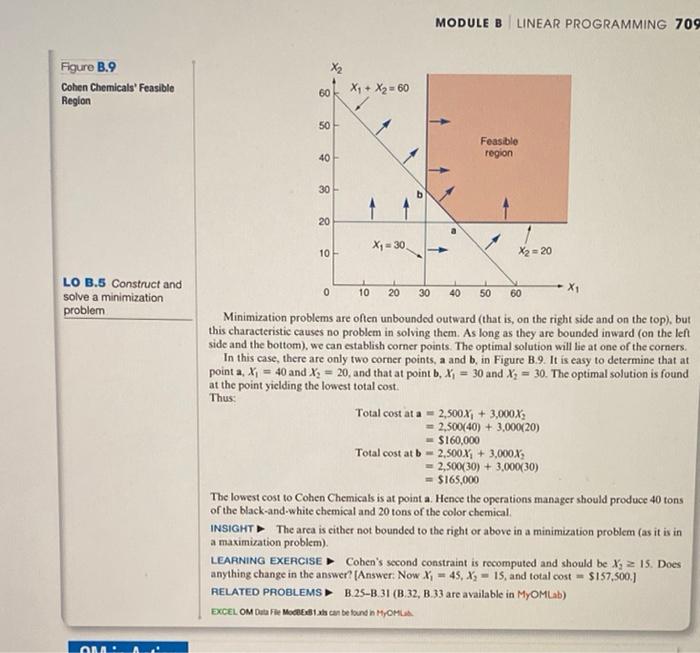
2. (5 points) Formulate and solve Cohen Chemicals, Example B1 from page 708 in the textbook. Use the layout used in the video. a What is the final value of the objective function? T b. What are the values of the decision variables? c. Which constraints are binding? d. What would you pay to relax each constraint? Example B1 A MINIMIZATION PROBLEM WITH TWO VARIABLES Cohen Chemicals, Inc., produces two types of photo-developing fluids. The first, a black-and-white picture chemical, costs Cohen $2,500 per ton to produce. The second, a color photo chemical, costs $3,000 per ton. Based on an analysis of current inventory levels and outstanding orders, Cohen's production man- ager has specified that at least 30 tons of the black-and-white chemical and at least 20 tons of the color chemical must be produced during the next month. In addition, the manager notes that an existing inventory of a highly perishable raw material needed in both chemicals must be used within 30 days. To avoid wasting the expensive raw material, Cohen must produce a total of at least 60 tons of the photo chemicals in the next month. APPROACH Formulate this information as a minimization LP problem Let: X; - number of tons of black-and-white photo chemical produced X; - number of tons of color photo chemical produced Objective: Minimize cost-$2,500x; + $3,000X; Subject to: Xi 2 30 tons of black-and-white chemical X = 20 tons of color chemical X1 + X: 260 tons total X, X, 20 nonnegativity requirements SOLUTION To solve the Cohen Chemicals problem graphically, we construct the problem's feasible region, shown in Figure B.9. 82% Page 708 of 808 . Location 18685 of 23024 MODULE B LINEAR PROGRAMMING 709 X2 Figure B.9 Cohen Chemicals' Feasible Region 60 X1 + Xz = 60 50 Feasible region 40 30 20 Xy = 30 10 X2 = 20 LO B.5 Construct and solve a minimization problem 0 10 20 30 40 50 60 Minimization problems are often unbounded outward (that is on the right side and on the top), but this characteristic causes no problem in solving them. As long as they are bounded inward (on the left side and the bottom), we can establish corner points. The optimal solution will lie at one of the corners. In this case, there are only two corner points, a and b. in Figure B.9. It is easy to determine that at point a, x1 = 40 and X; = 20, and that at point b, X; = 30 and X3 = 30. The optimal solution is found at the point yielding the lowest total cost. Thus: Total cost at a - 2,500X1 + 3,000X; = 2.500(40) + 3,000(20) $160,000 Total cost atb - 2,500X; + 3,000x3 2,500(30) + 3,000(30) $165,000 The lowest cost to Cohen Chemicals is at point a. Hence the operations manager should produce 40 tons of the black-and-white chemical and 20 tons of the color chemical INSIGHT The arca is either not bounded to the right or above in a minimization problem (as it is in a maximization problem). LEARNING EXERCISE Cohen's second constraint is recomputed and should be X215. Does anything change in the answer? [Answer: Now X; - 45, X; - 15, and total cost = $157,500.) RELATED PROBLEMS B.25-B 31 (B.32, B. 33 are available in MyOMLab) EXCEL OM Duta Fe MB1 cabe found in MYOMLA ORA. Variables X-pods: Blueberrys: Objective Function Max Profit = 7*X + 5*B Constraints Electronics: 4*X + 3*B 240 Assembly: 2*X + 1*B S 100 X 20: 20 B 20: B 20