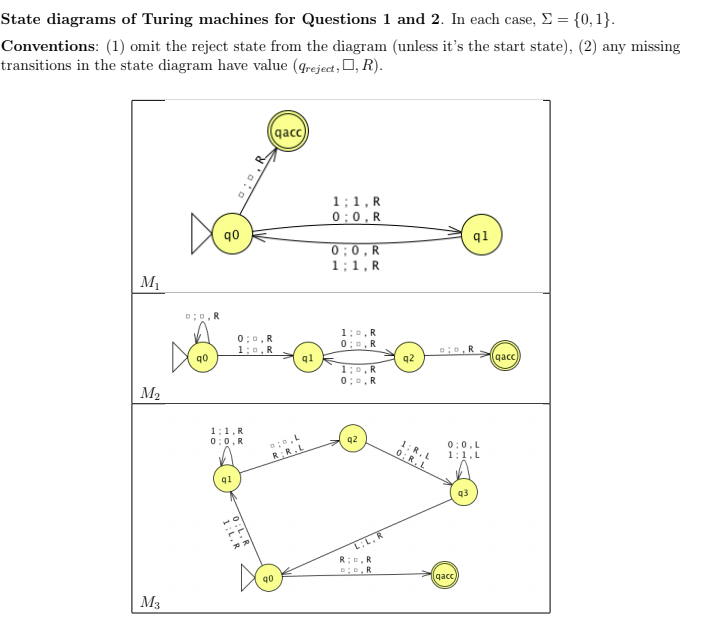
2. (8 points) Let M be an arbitrary Turing machine over a fixed alphabet . Consider the following two constructions . Construction 1: Suppose M Q. ., qo,gaccept, greject). We define the Turing machine M, as (Q...6,go, greject , qaccept Construction 2: We (try to) define the Turing machine M, as Mh-"On input w, 1. Run the Turing machine M on w 2. If M accepts w, reject. Otherwise, reject." (a) Apply Construction 1 to Mi from the first question in this warmup i. Does the resulting Turing machine recognize * \ L(M) ii. Is the resulting Turing machine a decider? (b) Apply Construction 1 to M2 from the first question in this warmup. Does the resulting Turing machine recognize * \ L(My)? i. Does the resulting Turing machine recognize * \ L(M2) ii. Is the resulting Turing machine a decider? (c) Apply Construction 1 to Ms from the first question in this warmup. Does the resulting Turing machine recognize * \ L(My)? i. Does the resulting Turing machine recognize * \ L(M) ii. Is the resulting Turing machine a decider? (d) The construction of Mh doesn't actually define a Turing machine. Which of these are problems with the construction (list all that apply) i. One Turing machine can't run another as a subroutine ii. The Turing machine M might not halt on the input w, so we can't run it in step 1 iii. The Turing machine M halts when it accepts or rejects so the computation of Mh will never get to step 2 would lead to a contradiction M may not be a decider iv. The conditional statement in step 2 isn't allowed to reject a string that it accepts, that v. The conditional statement's else branch in step 2 isn't executable in finite time since State diagrams of Turing machines for Questions 1 and 2 . In each case, (0,1} Conventions: (1) omit the reject state from the diagram (unless it's the start state), (2) any missing transitions in the state diagram have value (greject,D, R) qacc 1:1.R 0:0,R q0 1:1,R qo q2 qacc M2 1:1.R 0:0,R q2 0:0.L q1 g0 2. (8 points) Let M be an arbitrary Turing machine over a fixed alphabet . Consider the following two constructions . Construction 1: Suppose M Q. ., qo,gaccept, greject). We define the Turing machine M, as (Q...6,go, greject , qaccept Construction 2: We (try to) define the Turing machine M, as Mh-"On input w, 1. Run the Turing machine M on w 2. If M accepts w, reject. Otherwise, reject." (a) Apply Construction 1 to Mi from the first question in this warmup i. Does the resulting Turing machine recognize * \ L(M) ii. Is the resulting Turing machine a decider? (b) Apply Construction 1 to M2 from the first question in this warmup. Does the resulting Turing machine recognize * \ L(My)? i. Does the resulting Turing machine recognize * \ L(M2) ii. Is the resulting Turing machine a decider? (c) Apply Construction 1 to Ms from the first question in this warmup. Does the resulting Turing machine recognize * \ L(My)? i. Does the resulting Turing machine recognize * \ L(M) ii. Is the resulting Turing machine a decider? (d) The construction of Mh doesn't actually define a Turing machine. Which of these are problems with the construction (list all that apply) i. One Turing machine can't run another as a subroutine ii. The Turing machine M might not halt on the input w, so we can't run it in step 1 iii. The Turing machine M halts when it accepts or rejects so the computation of Mh will never get to step 2 would lead to a contradiction M may not be a decider iv. The conditional statement in step 2 isn't allowed to reject a string that it accepts, that v. The conditional statement's else branch in step 2 isn't executable in finite time since State diagrams of Turing machines for Questions 1 and 2 . In each case, (0,1} Conventions: (1) omit the reject state from the diagram (unless it's the start state), (2) any missing transitions in the state diagram have value (greject,D, R) qacc 1:1.R 0:0,R q0 1:1,R qo q2 qacc M2 1:1.R 0:0,R q2 0:0.L q1 g0