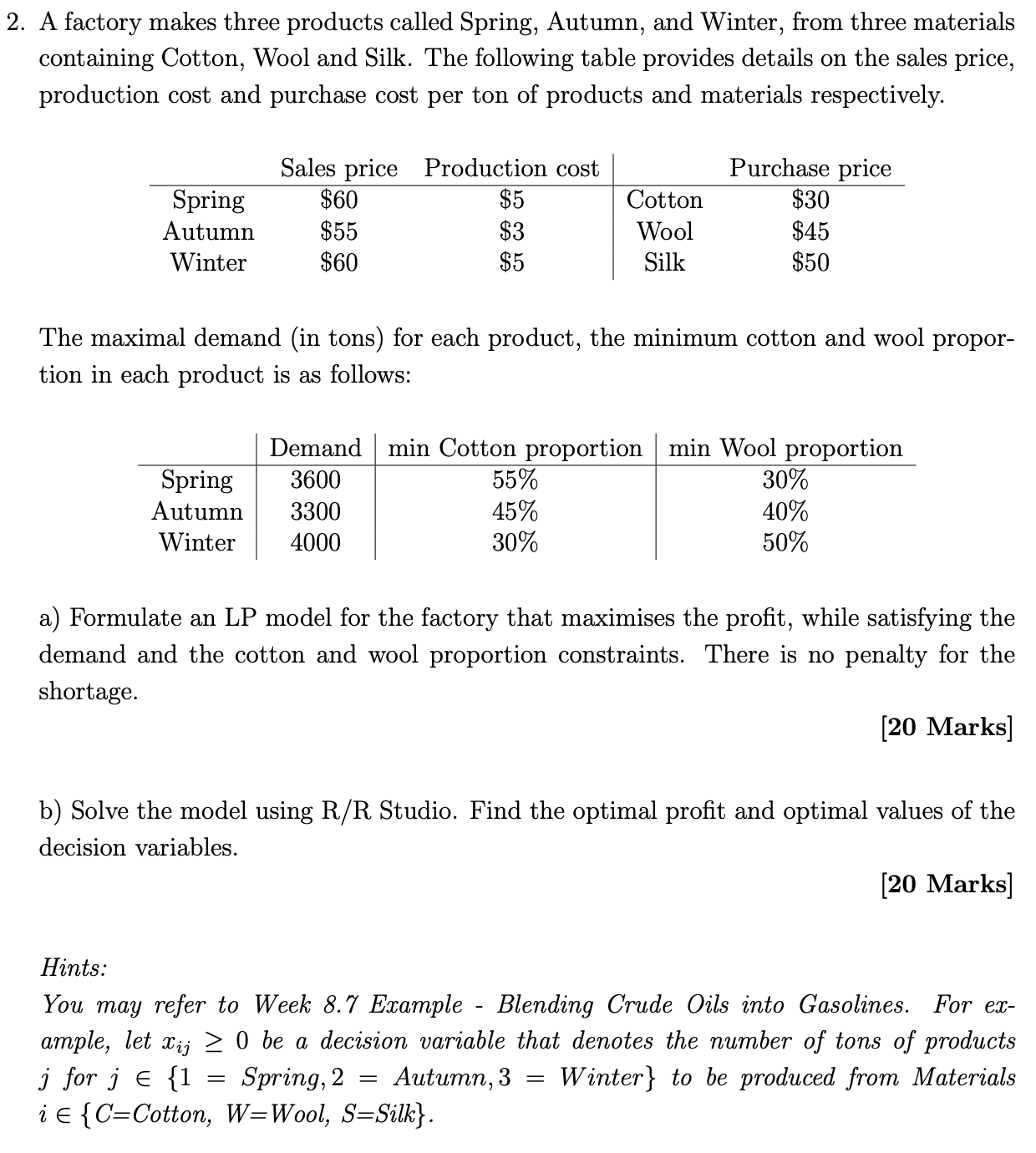
2. A factory makes three products called Spring, Autumn, and Winter, from three materials containing Cotton, Wool and Silk. The following table provides details on the sales price, production cost and purchase cost per ton of products and materials respectively. Sales price Production cost Purchase price Spring $60 $5 Cotton $30 Autumn $55 $3 Wool $45 Winter $60 $5 Silk $50 The maximal demand (in tons) for each product, the minimum cotton and wool propor- tion in each product is as follows: Demand | min Cotton proportion | min Wool proportion Spring 30% Autumn 40% Winter 50% a) Formulate an LP model for the factory that maximises the profit, while satisfying the demand and the cotton and wool proportion constraints. There is no penalty for the shortage. [20 Marks] b) Solve the model using R/R Studio. Find the optimal profit and optimal values of the decision variables. [20 Marks] Hints: You may refer to Week 8.7 Example - Blending Crude Oils into Gasolines. For ezx- ample, let x;; > 0 be a decision variable that denotes the number of tons of products j for j {1 = Spring,2 = Autumn,3 = Winter} to be produced from Materials i {C=Cotton, W=Wool, S=Silk}