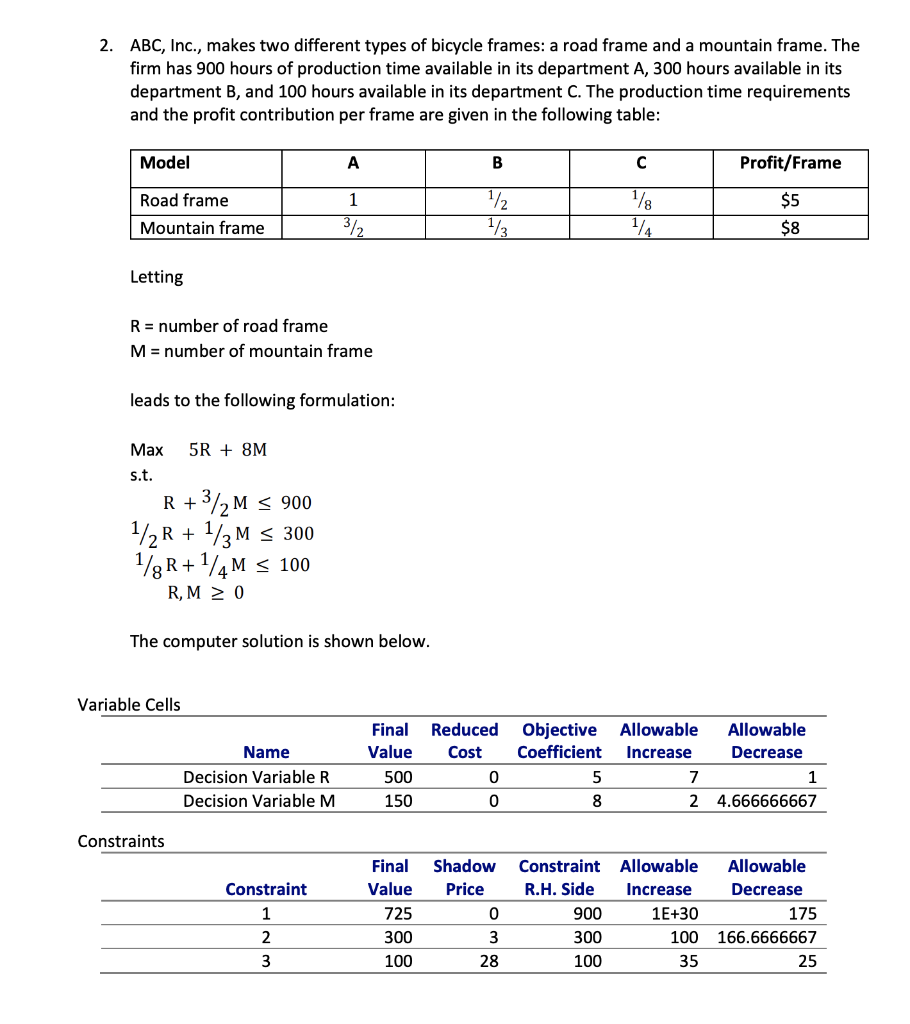
2. ABC, Inc., makes two different types of bicycle frames: a road frame and a mountain frame. The firm has 900 hours of production time available in its department A, 300 hours available in its department B, and 100 hours available in its department C. The production time requirements and the profit contribution per frame are given in the following table: Model B C Profit/Frame Road frame Mountain frame 1 372 1/2 1/3 1/8 1/4 $5 $8 Letting R = number of road frame M= number of mountain frame leads to the following formulation: 5R + 8M Max s.t. R + +3/2 M 900 1/2 R + 1/3 M S 300 1/8R+1/4M S 100 RM 20 The computer solution is shown below. Variable Cells Reduced Cost Name Decision Variable R Decision Variable M Final Value 500 150 Objective Allowable Allowable Coefficient Increase Decrease 5 7 1 8 24.666666667 0 0 Constraints Constraint 1 Final Value 725 Shadow Price 0 Constraint Allowable R.H. Side Increase 900 1E+30 300 100 100 35 Allowable Decrease 175 166.6666667 25 2 3 300 100 3 28 a) [1 mark] What is the optimal solution, and what is the value of the total profit contribution? b) [2 marks] Which constraints are binding? c) [3 marks] If overtime can be scheduled in one of the departments, where would you recommend doing so? d) [3 marks] How much will the value of the optimal solution improve if 20 extra hours of time are made available in department C? e) [2 marks] ABC is con dering reducing the price of road frame such that the ne contribution to profit is $2.99 per frame. How would this change in price affect the optimal solution? Explain. f) [2 marks] If the available production time in its department B is increased by 50 hours, will the dual value for the manufacturing time constraint change? Explain. 2. ABC, Inc., makes two different types of bicycle frames: a road frame and a mountain frame. The firm has 900 hours of production time available in its department A, 300 hours available in its department B, and 100 hours available in its department C. The production time requirements and the profit contribution per frame are given in the following table: Model B C Profit/Frame Road frame Mountain frame 1 372 1/2 1/3 1/8 1/4 $5 $8 Letting R = number of road frame M= number of mountain frame leads to the following formulation: 5R + 8M Max s.t. R + +3/2 M 900 1/2 R + 1/3 M S 300 1/8R+1/4M S 100 RM 20 The computer solution is shown below. Variable Cells Reduced Cost Name Decision Variable R Decision Variable M Final Value 500 150 Objective Allowable Allowable Coefficient Increase Decrease 5 7 1 8 24.666666667 0 0 Constraints Constraint 1 Final Value 725 Shadow Price 0 Constraint Allowable R.H. Side Increase 900 1E+30 300 100 100 35 Allowable Decrease 175 166.6666667 25 2 3 300 100 3 28 a) [1 mark] What is the optimal solution, and what is the value of the total profit contribution? b) [2 marks] Which constraints are binding? c) [3 marks] If overtime can be scheduled in one of the departments, where would you recommend doing so? d) [3 marks] How much will the value of the optimal solution improve if 20 extra hours of time are made available in department C? e) [2 marks] ABC is con dering reducing the price of road frame such that the ne contribution to profit is $2.99 per frame. How would this change in price affect the optimal solution? Explain. f) [2 marks] If the available production time in its department B is increased by 50 hours, will the dual value for the manufacturing time constraint change? Explain