Question: 2) Assume that the random vector X = (X, Y) has covariance matrix COV[X]. Assume E[X] = E[Y] = 0. a) Why do the eigenvectors

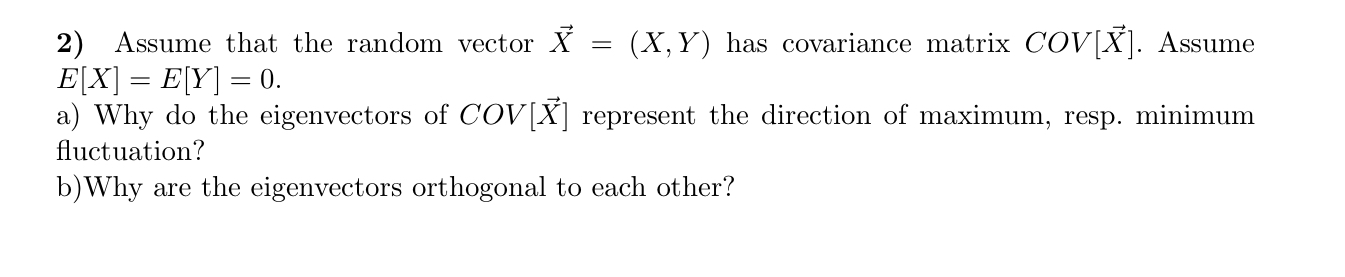
2) Assume that the random vector X = (X, Y) has

2) Assume that the random vector X = (X, Y) has covariance matrix COV[X]. Assume E[X] = E[Y] = 0. a) Why do the eigenvectors of COV[X] represent the direction of maximum, resp. minimum fluctuation? b) Why are the eigenvectors orthogonal to each other

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

please help me answer this question , thanks ! Problem 3: Do Regressions Make Sense? [Remark: Without the knowledge of convergence of random variables, one cannot "prove" the statements above...

The average velocity of blood flowing in a certain 4 mm diameter artery in the human body is 0.28 m/s. Calculate the Reynolds number and determine whether the flow is laminar or turbulent. The...

solve these practice problems Suppose the sediment density (g/cm) of a randomly selected specimen from a certain region is normally distributed with mean 2.65 and standard deviation .85 (suggested in...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Problem 11.5 (*). We consider here a simple portfolio optimization problem. Assume that we can invest in n financial assets. Each asset i has a return of Xi (X; is a random variable) meaning that...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

please help with the following questions 5.108. Let h(x, y) be a joint Gaussian pdf for zero-mean, unit-variance Gaussian random vari- ables with correlation coefficient p . Let g(x, y) be a joint...

space weather PLEASE HELP ME use MATLAB NO REFERENCE 1.1 Free Space Maxwell's equations describe the behavior of electromagnetic fields and their interaction with mat- ter. They are one of the major...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Use the result obtained in Problem 45(a) to calculate the electric field along the axis of the disk. Then calculate the electric field by direct integration using Coulomb's law.

Kitt Company borrows $ 800,000 from Neville Capital by issuing an 8- year (96- month), 12% note payable. Interest is due and payable each month based on the outstanding balance at the beginning of...

Press to start a slide show from the beginning of a presentation. A . F 1 2 B . F 5 C . F 1 1 D . F 1

The compound you identified in Problem 7 is a metabolic regulator. Predict its effect on (a) hexokinase and (b) PFK.

A Dutch investor holds a portfolio of Japanese stocks worth 160 million. The current three-month dollar/euro forward exchange rate is $1.2/, and the current three-month $: forward exchange rate is...

The manager of a crew that installs carpets has tracked the crews output over the past several weeks, obtaining these figures: Calculate the labour productivity for each of the weeks. On the basis of...

A typical Japanese automobile manufacturing plant in North America produces more cars with fewer workers than a typical Big 3 North American plant; see, for example, vrww....

Use the horizontal model, or write the journal entry, for each of the following transactions and adjustments that occurred during the first year of operations at Kissick Co. a. Issued 100,000 shares...

An area in Toronto is being considered for development into a housing project with a small playground for the kids. In the soil and ground water shows high levels of heavy metals (nickel, lead,...

2. Find out if there are other reference points that can be used as reasonable alternatives.

1. Identify your reference point when making a decision based on an element of risk.

3. If there are reasonable alternatives, think about your decisions based on the different reference points and see if there are any contradictions in the decisions.